题目内容
【题目】如图,点P是∠MON内的一点,过点P作PA⊥OM于点A,PB⊥ON于点B,且OA=OB.
(1)求证:PA=PB;
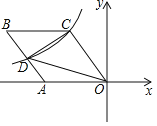
(2)如图②,点C是射线AM上一点,点D是线段OB上一点,且∠CPD+∠MON=180°,若OC=8,OD=5.求线段OA的长.
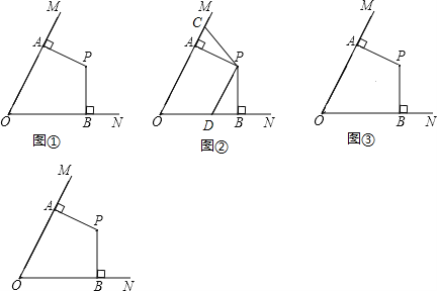
(3)如图③,若∠MON=60°,将PB绕点P以每秒2°的速度顺时针旋转,12秒后,PA开始绕点P以每秒10°的速度顺时针旋转,PA旋转270°后停止,此时PB也随之停止旋转.旋转过程中,PA所在直线与OM所在直线的交点记为G,PB所在直线与ON所在直线的交点记为H.问PB旋转几秒时,PG=PH?
【答案】(1)见解析;(2)OA=6.5;(3)满足条件的t的值为15s或25s或37.5s.
【解析】
(1)如图1中,连接OP,证明Rt△OPA≌Rt△OPB(HL)即可解决问题.
(2)如图②中,想办法证明OC+OD=2OA即可解决问题.
(3)设点P的旋转时间为t秒.分四种情形①当0<t<12时,不存在.②当12≤t<21时,如图3-1中.③当21≤t<30时,如图3-2中.④当30≤t<39时,如图3-3中,分别求解即可解决问题.
(1)证明:如图①中,连接OP.
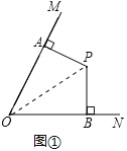
∵PA⊥OM,PB⊥ON,
∴∠OAP=∠OBP=90°,
∵OA=OB,OP=OP,
∴Rt△OPA≌Rt△OPB(HL),
∴PA=PB.
(2)如图②中,
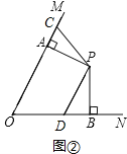
∵∠PAO=∠PBO=90°,
∴∠AOB+∠APB=180°,
∵∠CPD+∠AOB=180°,
∴∠CPD=∠APB,
∴∠APC=∠BPD,
∵PA=PB,∠PAC=∠PBD=90°,
∴△PAC≌△PBD(ASA),
∴AC=BD,
∴OC+OD=OA+AC+OB-BD=2OA=13,
∴OA=6.5.
(3)设点P的旋转时间为t秒.
①当0<t<12时,此时只有PB旋转,PA没有旋转,故不存在PG=PH.
②当PA旋转的度数为0°—90°时,时间t的取值为:12≤t<21;
∴当12≤t<21时,如图3-1中,∠APG=(10t-120)°,∠BPH=2t°,
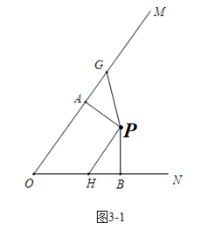
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t-120=2t,
∴t=15.
③当PA旋转的度数为90°—180°时,时间t的取值为:21≤t<30,
∴当21≤t<30时,如图3-2中,∠APG=180°-∠APA′=180°-(10t-120)°=(300-10t)°,∠BPH=2t,
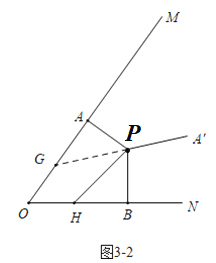
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时300-10t=2t,
∴t=25.
④当PA旋转的度数为180°—270°时,时间t的取值为:30≤t<39;
当30≤t<39时,如图3-3中,∠APG=(10t-300)°,∠BPH=2t,
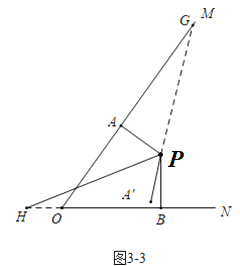
当∠APG=∠BPH时,△PAG≌△PBH,可得PG=PH,
此时10t-300=2t,
∴t=37.5;
综上所述,满足条件的t的值为15s或25s或37.5s.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案