题目内容
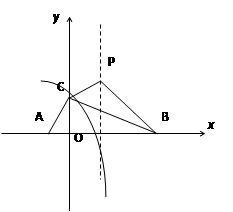
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
【答案】
(1)解:连接DE, 
∵y=x2﹣2x﹣3,
∴x=0时,y=﹣3,
y=0时,x1=﹣1,x2=3,
∴点A的坐标为(﹣1,0),点B的坐标为(0,﹣3),点C的坐标为(3,0),
∵AC=4,
∴AE=DE=2,
∴OE=1,
∴OD= ![]() =
= ![]() ,
,
∴D点的坐标为(0, ![]() )
)
(2)解:∵DF是果圆的切线,
∴ED⊥DF,又DO⊥EF,
∴DE2=EOEF,
∴EF=4,则OF=3,
∴点F的坐标为(﹣3,0),
设经过点D的果圆的切线DF的解析式为y=kx+b,
则 ![]() ,
,
解得 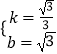 .
.
∴经过点D的果圆的切线DF的解析式为y= ![]() x+
x+ ![]()
(3)解:设经过点B的果圆的切线的解析式为:y=ax+c,
∵点B的坐标为(0,﹣3),
∴经过点B的果圆的切线的解析式为:y=ax﹣3,
由题意得,方程组 ![]() 只有一个解,
只有一个解,
即一元二次方程x2﹣(a+2)x=0有两个相等的实数根,
△=(a+2)2﹣4×1×0=0,
解得a=﹣2,
∴经过点B的果圆的切线的解析式为:y=﹣2x﹣3,
当y=0时,x=﹣ ![]() ,
,
∴点M的坐标为(﹣ ![]() ,0),即OM=
,0),即OM= ![]() ,
,
∴△OBM的面积= ![]() ×OM×OB=
×OM×OB= ![]() .
.
【解析】(1)连接DE, 根据坐标轴上点的坐标特点求出A,B,C三点的坐标,根据A,C两点的坐标求出半圆直径AC的长,从而得出半径AE=DE=2,算出OE的长,根据勾股定理得出OD的长,从而得出D点的坐标;
(2)根据切线的性质得出ED⊥DF,又DO⊥EF,从而判断出△OED![]() △DEF,根据相似三角形对应边成比例得出DE2=EOEF,从而得出点F的坐标,设经过点D的果圆的切线DF的解析式为y=kx+b,用待定系数法求出经过点D的果圆的切线DF的解析式;
△DEF,根据相似三角形对应边成比例得出DE2=EOEF,从而得出点F的坐标,设经过点D的果圆的切线DF的解析式为y=kx+b,用待定系数法求出经过点D的果圆的切线DF的解析式;
(3)设经过点B的果圆的切线的解析式为:y=ax+c,由于直线过点B,故经过点B的果圆的切线的解析式为:y=ax﹣3,由于y=ax﹣3与y=x2﹣2x﹣3组成的方程组只有一个解,即一元二次方程x2﹣(a+2)x=0有两个相等的实数根,由根的判别式(a+2)2﹣4×1×0=0,得出a的值,从而得出经过点B的果圆的切线的解析式为:y=﹣2x﹣3,进而找到M点的坐标,求出△OBM的面积。
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 名校课堂系列答案
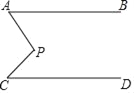
名校课堂系列答案【题目】如图,AB∥CD,∠A=50°,∠C=45°,求∠P的度数.
下面提供三种思路:
(1)过P作FG∥AB
(2)延长AP交直线CD于M;
(3)延长CP交直线AB于N.
请选择两种思路,求出∠P的度数.