题目内容
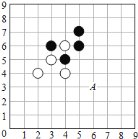
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.现从点
的中点.现从点![]() 观察线段
观察线段![]() ,当长度为
,当长度为![]() 的线段
的线段![]() (图中的黑粗线)以每秒
(图中的黑粗线)以每秒![]() 个单位长的速度沿线段
个单位长的速度沿线段![]() 从左向右运动时,
从左向右运动时,![]() 将阻挡部分观察视线,在
将阻挡部分观察视线,在![]() 区域内形成盲区.设
区域内形成盲区.设![]() 的左端点从
的左端点从![]() 点开始,运动时间为
点开始,运动时间为![]() 秒
秒![]() .设
.设![]() 区域内的盲区面积为
区域内的盲区面积为![]() (平方单位).
(平方单位).

![]() 求
求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
![]() 请简单概括
请简单概括![]() 随
随![]() 的变化而变化的情况.
的变化而变化的情况.
【答案】(1)![]() 时,
时,![]() ,
,![]() 时,
时,![]() ,
,![]() 时,
时,![]() ;(2)
;(2)![]() 秒内,
秒内,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 秒到
秒到![]() 秒,
秒,![]() 的值不变;
的值不变;![]() 秒到
秒到![]() 秒,
秒,![]() 随
随![]() 的增大而减小.
的增大而减小.
【解析】
(1)根据正方形的性质得AM=2,盲区为梯形,且上底为下底的一半,高为2,然后分段计算:当0≤t≤1时,梯形的上底为t,则下底为2t;当1<t≤2时,梯形的上底为1,下底为2;当2<t≤3时,梯形的上底为1-(t-2)=3-t,则下底为2(3-t),然后根据梯形的面积分别计算出三中情况下的梯形的面积即可;
(2)根据一次函数的性质求解.
![]() ∵正方形
∵正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,
的中点,
∴![]() ,盲区为梯形,且上底为下底的一半,高为
,盲区为梯形,且上底为下底的一半,高为![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]()
![]() ;
;
(2)![]() 秒内,
秒内,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 秒到
秒到![]() 秒,
秒,![]() 的值不变;
的值不变;![]() 秒到
秒到![]() 秒,
秒,![]() 随
随![]() 的增大而减小.
的增大而减小.

练习册系列答案
相关题目