题目内容
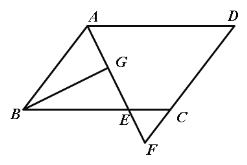
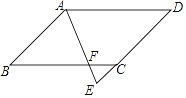
【题目】如图,四边形ABCD是平行四边形,AE平分∠BAD,交DC的延长线于点E,AB=3,EF=0.8,AF=2.4.求AD的长.
【答案】4
【解析】
由平行四边形的性质得出AB∥CD,则△ABF∽△ECF,由该相似三角形的对应边成比例求得CE=1;由AB∥CD得出内错角相等∠E=∠BAE,再由角平分线等量代换证出∠E=∠DAE,即可得出结论AD=DE=4.
解:∵四边形ABCD为平行四边形,
∴AB=DC=3,AB∥DE,
∴△ABF∽△ECF,
∴ ![]() =
=![]() .
.
∵AB=3,EF=0.8,AF=2.4,
∴ ![]() ,
,
∴CE=1,
∴DE=DC+CE=3+1=4.
∵AB∥DE,
∴∠BAE=∠E.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
∴∠E=∠DAE.
∴AD=DE=4.
∴AD的长为4.

练习册系列答案
相关题目
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 |
| ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=![]() 有 个实数根;
有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .