��Ŀ����
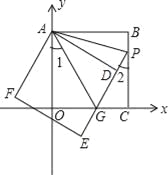
����Ŀ����ͼ��������ABCO�ı�OA��OC���������ϣ���B����Ϊ��3��3������������ABCO�Ƶ�A˳ʱ����ת�Ƕ�����0��������90�������õ�������ADEF��ED���߶�OC�ڵ�G��ED���ӳ��߽��߶�BC�ڵ�P����AP��AG��
��1����֤����AOG�ա�ADG��
��2������PAG�Ķ��������ж��߶�OG��PG��BP֮���������ϵ��˵�����ɣ�
��3������1=��2ʱ����ֱ��PE�Ľ���ʽ��
��4���ڣ�3���������£�ֱ��PE���Ƿ���ڵ�M��ʹ��M��A��GΪ������������ǵ��������Σ������ڣ���ֱ��д��M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1)֤�����̼�������(2)PG=OG+BP�����ɼ�������(3)y=![]() x��3��(4)��0����3����2
x��3��(4)��0����3����2![]() ��3����
��3����
�����������������(1)��AO=AD��AG=AG������б�ߺ�һ��ֱ�DZ߶�Ӧ��ȵ�����ֱ��������ȫ�ȣ��жϳ���AOG�ա�ADG���ɣ�(2)���ȸ���������ȫ�ȵ��ж��������жϳ���ADP�ա�ABP���ٽ����AOG�ա�ADG���ɵ���DAP=��BAP����1=��DAG��Ȼ�������1+��DAG+��DAP+��BAP=90���������PAG�Ķ���������жϳ��߶�OG��PG��BP֮���������ϵ���ɣ�(3)���ȸ�����AOG�ա�ADG���жϳ���AGO=��AGD��Ȼ�������1+��AGO=90������2+��PGC=90�����жϳ�����1=��2ʱ����AGO=��AGD=��PGC������AGO+��AGD+��PGC=180���������1=��2=30�������ȷ����P��G�������꣬�����жϳ�ֱ��PE�Ľ���ʽ��
(4)�������⣬�����������������M��x��ĸ�������ʱ��������M��EP���ӳ�����ʱ��������M��A��GΪ������������ǵ��������Σ����M�������Ƕ��ټ��ɣ�
���������(1)��Rt��AOG��Rt��ADG�У�![]() ��HL�� ���AOG�ա�ADG��
��HL�� ���AOG�ա�ADG��
(2)��Rt��ADP��Rt��ABP�У�![]() ���ADP�ա�ABP�� ����DAP=��BAP��
���ADP�ա�ABP�� ����DAP=��BAP��
�ߡ�AOG�ա�ADG�� ���1=��DAG�� ���ߡ�1+��DAG+��DAP+��BAP=90����
��2��DAG+2��DAP=90���� ���DAG+��DAP=45���� �ߡ�PAG=��DAG+��DAP�� ���PAG=45����
�ߡ�AOG�ա�ADG�� ��DG=OG�� �ߡ�ADP�ա�ABP�� ��DP=BP�� ��PG=DG+DP=OG+BP��
(3)�⣺�ߡ�AOG�ա�ADG�� ���AGO=��AGD�� ���ߡ�1+��AGO=90������2+��PGC=90������1=��2��
���AGO=��PGC�� ���ߡ�AGO=��AGD�� ���AGO=��AGD=��PGC��
���ߡ�AGO+��AGD+��PGC=180���� ���AGO=��AGD=��PGC=180���3=60����
���1=��2=90�㩁60��=30���� ��Rt��AOG�У� ��AO=3�� ��OG=AOtan30��=3��![]() =
=![]() ��
��
��G��������![]() ��0����CG=3��
��0����CG=3��![]() �� ��Rt��PCG��PC=
�� ��Rt��PCG��PC=![]() =
=![]() =3��
=3��![]() ��1����
��1����
��P������Ϊ����3��3![]() ��3 ���� ��ֱ��PE�Ľ���ʽΪ��y=kx+b�� ��
��3 ���� ��ֱ��PE�Ľ���ʽΪ��y=kx+b�� �� ��
��
��ã� �� ��ֱ��PE�Ľ���ʽΪy=
�� ��ֱ��PE�Ľ���ʽΪy=![]() x��3��
x��3��
(4)����ͼ/span>1������M��x��ĸ�������ʱ���� ��AG=MG����A����Ϊ��0��3����
����M������0����3����


����ͼ2������M��EP���ӳ�����ʱ���� �ɣ�3�����ɵ���AGO=��PGC=60����
��EP��AB�Ľ���M������AG=MG�� ��A��ĺ�������0��G�������Ϊ![]() ��
��
��M�ĺ�������2![]() ����������3�� ����M����Ϊ��2
����������3�� ����M������2![]() ��3����
��3����
���ϣ��ɵ� ��M����Ϊ��0����3����2![]() ��3����
��3����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�