题目内容
【题目】如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB，AC于M，N两点，以点D为中心旋转∠MDN(∠MDN的度数不变)，若DM与AB垂直时(如图①所示)，易证BM +CN =BD.
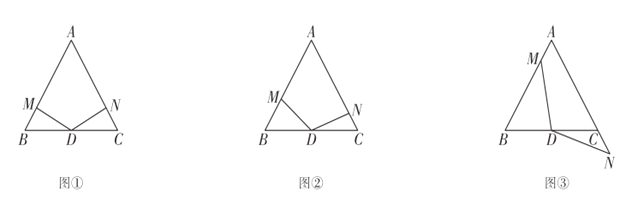
（1）如图②，若DM与AB不垂直时，点M在边AB上，点N在边AC上，上述结论是否成立?若成立，请给予证明;若不成立，请说明理由；
（2）如图③，若DM与AB不垂直时，点M在边AB.上，点N在边AC的延长线上，上述结论是否成立?若不成立，请写出BM，CN，BD之间的数量关系，不用证明.
【答案】（1）成立，见解析；（2）图③的结论不成立.图③的结论为BM-CN = BD.
【解析】
（1）根据等边三角形的性质，及过D作DE平行AC交AB于E点，构造△DME与△DNC全等，利用全等三角形的对应边相等及线段的和差关系给予证明.（2）利用同（1）的方法构造全等，根据和差关系得出的结论为BM-CN = BD.
(1)证明:图②的结论成立，为BM +CN = BD.理由如下：
如图，过点D作DE//AC交AB于点E.
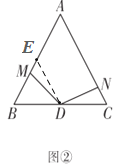
∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°.
∵DE//AC，
∴∠BED=∠BDE =∠A=∠C=∠B= 60°，
∴△BDE是等边三角形，
∴∠EDC = 120°.
∴∠EDN +∠NDC= 120°.
∵∠MDN= 120°，
∴∠EDN十∠MDE = 120°，
∴∠NDC=∠MDE.
∵D是BC的中点，
∴BD = DC，
∴BD=DE = DC.
∵∠BED=∠C =60°
∴△DME≌△DNC.
∴ME = NC，
∴BM十ME= BE，
∴BM十CN= BD.
(2)解:图③的结论不成立.正确结论为BM-CN = BD.理由如下：
如图，过点D作DF//AC交AB于点F.
∵△ABC是等边三角形，
∴∠A=∠B=∠ACB=60°,
∴DF//AC，
∴∠BFD=∠BDF=∠A=∠ACB =∠B = 60°.,
∴△BDF是等边三角形，
∴∠FDC =∠MFD=∠DCN=120°，
∴∠FDM +∠MDC= 120°.
∵∠MDN= 120°，
∴∠MDC十∠NDC = 120°,
∴∠NDC=∠FDM.
∵D是BC的中点，
∴BD = DC,
∴BD=DF = DC.
∵∠MFD=∠DCN=120°,
∴△DMF≌△DNC,
∴MF = NC,
∴BM-MF =BF ,
∴BM-CN =BD .
