题目内容
【题目】已知抛物线：y＝x2+bx+c
（1）若抛物线过点（2，﹣3），（4，5），求b、c．
（2）若抛物线过（﹣1，m2﹣m），（2，m2+2m），且﹣5≤m≤﹣3，求在m的变化过程中，抛物线最低点的坐标．
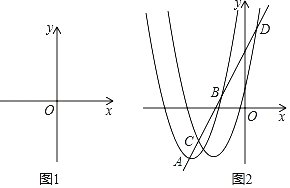
（3）直线y＝2x+n与抛物线y＝x2+bx+c交于A（﹣5，yA），B（﹣3，yB），把y＝x2+bx+c向右平移t个单位（t＞0）后交直线y＝2x+n于C、D两点，若CD＝2AB，求t的值．
【答案】（1）
；（2）（2，3）；（3）t
．
【解析】
（1）将点（2，﹣3），（4，5）代入二次函数表达式，即可求解；
（2）同理可得：y＝x2+（m﹣1）x+（m2﹣2），函数的对称轴为：x
，函数在顶点处取得最小值，则顶点的坐标为（
，
），即可求解；
（3）将直线y＝2x+n与抛物线y＝x2+bx+c联立并整理得：x2+（b﹣2）x+（c﹣n）＝0，求出b＝10，c﹣n＝15；同理：由x2+（b﹣2）x+（c﹣2t﹣n）＝0，即x2+8x+（15﹣2t）＝0，
则x1+x2＝﹣8，x1x2＝15﹣2t，CD＝2AB，x2﹣x1＝2×（﹣3+5）＝4
，即可求解．
解：（1）将点（2，﹣3），（4，5）代入二次函数表达式得：
，解得：
，
故函数的表达式为：y＝x2﹣2x﹣3…①；
（2）将（﹣1，m2﹣m），（2，m2+2m）代入二次函数表达式，
同理可得：y＝x2+（m﹣1）x+（m2﹣2），函数的对称轴为：x，
函数在顶点处取得最小值，则顶点的坐标为（，），
当﹣5≤m≤﹣3时，
设S
，该函数的对称轴为m
，
故函数S在m＝﹣3时取得最小值，即m＝﹣3，
则最低点即函数顶点坐标为（2，3）；
（3）将直线y＝2x+n与抛物线y＝x2+bx+c联立并整理得：
x2+（b﹣2）x+（c﹣n）＝0，
由韦达定理得：（﹣3）+（﹣5）＝2﹣b，（﹣3）（﹣5）＝c﹣n，
解得：b＝10，c﹣n＝15；
将直线向左平移t个单位后于抛物线交点的情况和题设中平移的方式交点情况应该相同，
即设抛物线不动、直线向左平移t个单位交点于点C′、D′和上述平移的C、D交点情况相同，
直线向左平移t个单位后的表达式为：y＝2（x+t）+n…②，
联立①②并整理得：x2+（b﹣2）x+（c﹣2t﹣n）＝0，即x2+8x+（15﹣2t）＝0，
则x1+x2＝﹣8，x1x2＝15﹣2t，
∵CD＝2AB，∴x2﹣x1＝2×（﹣3+5）＝4，
解得：t
．
