题目内容
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x交于A,B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C,D两点,D点在x轴下方且横坐标小于3,则下列结论错误的是( )
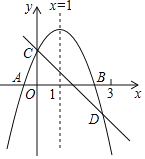
A.2a+b+c>0
B.a<﹣1
C.x(ax+b)≤a+b
D.双曲线y=![]() 的两分支分别位于第一、第三象限
的两分支分别位于第一、第三象限
【答案】D
【解析】
A、根据抛物线与y轴的交点在x轴上方可得c>0,由抛物线的对称轴为直线x=1可得b=﹣2a,进而可判断2a+b+c的符号;
B、根据图象可知当x=3时,一次函数值比二次函数值大,即9a+3b+c<﹣3+c,再把b=﹣2a代入即可判断;
C、根据图象可知当x=1时,二次函数有最大值,即ax2+bx+c≤a+b+c,从而可得ax2+bx≤a+b;
D、根据题意并结合二次函数的对称性可知抛物线与x轴的另一个交点在点(﹣1,0)右侧,从而得当x=﹣1时,y<0,即a﹣b+c<0,再根据反比例函数的性质即可判断.
解:∵抛物线与y轴的交点在x轴上方,
∴c>0,
∵抛物线的对称轴为直线x=﹣![]() =1,
=1,
∴b=﹣2a,
∴2a+b+c=2a﹣2a+c=c>0,所以A正确,不符合题意;
∵直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,
∴x=3时,一次函数值比二次函数值大,
即9a+3b+c<﹣3+c,
而b=﹣2a,
∴9a﹣6a<﹣3,解得a<﹣1,
所以B正确,不符合题意;
∵x=1时,二次函数有最大值,
∴ax2+bx+c≤a+b+c,
∴ax2+bx≤a+b,
所以C正确,不符合题意;
∵抛物线与x轴的一个交点在点(3,0)左侧,
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点在点(﹣1,0)右侧,
∴当x=﹣1时,y<0,
∴a﹣b+c<0,
∴双曲线y=![]() 的两分支分别位于第二、第四象限
的两分支分别位于第二、第四象限
所以D错误,符合题意,
故选D.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案