题目内容
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
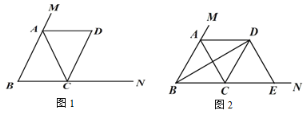
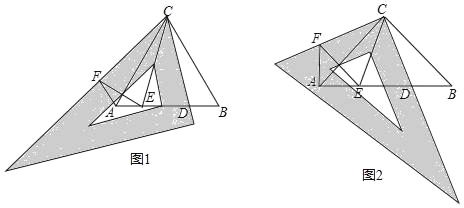
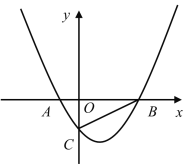
(1)如图 1,求证:四边形 ABCD 是平行四边形;
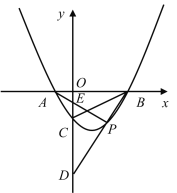
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
【答案】(1)见解析;(2)△ABC、△DBC、△ABD、△ACD.
【解析】
(1)根据等腰三角形的性质和三角形外角的性质可得∠CAM=2∠ABC,根据角平分线的定义可得∠CAM=2∠MAD,等量代换得到∠ABC=∠MAD,进而证得AD∥BC即可解决问题;
(2)首先证明平行四边形ABCD是菱形,然后证明△DCE是等边三角形,得到CE=CD=BC=AD,根据等底等高的三角形面积相等可得答案.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∴∠CAM=∠ABC+∠ACB=2∠ABC,
∵AD是∠CAM 的平分线,
∴∠CAM=2∠MAD,
∴∠ABC=∠MAD,
∴AD∥BC,
∵CD∥AB,
∴四边形ABCD是平行四边形;
(2)∵∠ABC=60°,AB=AC,四边形ABCD是平行四边形,
∴△ABC是等边三角形,∠DCE=∠ABC=60°,
∴AB=BC,
∴平行四边形ABCD是菱形,
∴∠DBE=30°,
∵DE⊥BD,
∴∠DEB=60°,
∴△DCE是等边三角形,
∴CE=CD=BC=AD,
∵AD∥BC,
∴△ABC、△DBC、△ABD、△ACD的面积都与△CDE的面积相等.

 阅读快车系列答案
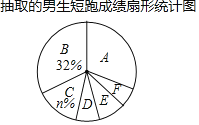
阅读快车系列答案【题目】中国飞人苏炳添以6秒47获得2019年国际田联伯明翰室内赛男子60米冠军,苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平,全校八年级男生中随机抽取了部分男生,对他们的短跑水平进行测试,并将测试成绩(满分10分)绘制成如下不完整的统计图表:
组别 | 成绩/分 | 人数/人 |
A | 5 | 36 |
B | 6 | 32 |
C | 7 | 15 |
D | 8 | 8 |
E | 9 | 5 |
F | 10 | m |
请你根据统计图表中的信息,解答下列问题:
(1)填空:m=_____,n=_____;
(2)所抽取的八年级男生短跑成绩的众数是_____分,扇形统计图中E组的扇形圆心角的度数为____°;
(3)求所抽取的八年级男生短跑的平均成绩.