Question

【题目】如图，已知抛物线y＝ax2＋bx＋c经过点A(－1，0)，点B(3，0)和点C(0，3)．

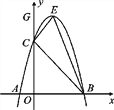
(1)求抛物线的解析式和顶点E的坐标；

(2)点C是否在以BE为直径的圆上?请说明理由；

(3)点Q是抛物线对称轴上一动点，点R是抛物线上一动点，是否存在点Q、R，使以Q、R、C、B为顶点的四边形是平行四边形?若存在，直接写出点Q、R的坐标，若不存在，请说明理由．

Answer 1

【答案】（1）y＝－x2＋2x＋3，E (1，4)；（2）在；（3）Q1(1，－2)，R1(4，－5)；

Q2(1，－8)，R2(－2，－5)；R3(2，3)，Q3(1，0)．

【解析】试题分析：（1）运用待定系数法即可得出函数关系式，然后进行配方即可得出顶点坐标；

（2）过点E分别作x轴、y轴的垂线，垂足分别F、G．易证△BCE为直角三角形，点C在以BE为直径的圆上；

（3）利用平行四边形的性质易得点Q、R的坐标.

试题解析： (1) 将A(－1，0)，B(3，0)和C(0，3)代入y=ax2＋bx＋c

得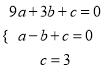

解得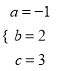

∴抛物线的解析式为y=－x2＋2x＋3，

∵y=－x2＋2x＋3=-（x-1）2+4，

∴顶点E的坐标为(1，4)．

(2)点C在以BE为直径的圆上，理由如下：

如图，过点E分别作x轴、y轴的垂线，垂足分别F、G．

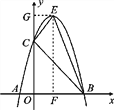
在Rt△BOC中，OB=3，OC=3，∴BC2=18

在Rt△CEG中，EG=1，CG=OG－OC=4－3=1，∴CE2=2

在Rt△BFE中，FE=4，BF=OB－OF=3－1=2， ∴BE2=20

∴BC2＋CE2=BE2

故△BCE为直角三角形，点C在以BE为直径的圆上．

(3)存在，点Q、R的坐标分别为Q1(1，－2)，R1(4，－5)；

Q2(1，－8)，R2(－2，－5)；R3(2，3)，Q3(1，0)．