题目内容
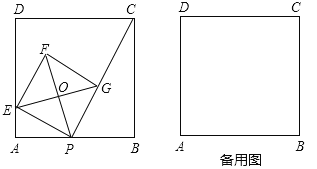
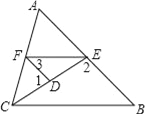
【题目】如图,已知∠1,∠2互为补角,且∠3=∠B,
(1)求证:∠AFE=∠ACB
(2)若CE平分∠ACB,且∠1=80°,∠3=45°,求∠AFE的度数.
【答案】(1)详见解析;(2)70°.
【解析】
(1)求出DF∥AB,推出∠3=∠AEF,求出∠B=∠AEF,得出FE∥BC,根据平行线性质求出即可;
(2)求出∠FED=80°-45°=35°,根据平行线性质求出∠BCE=∠FED=35°,求出∠ACB=2∠BCE=70°,根据平行线性质求出即可.
解:(1)因为∠1+∠FDE=180°,∠1,∠2互为补角,
所以∠2=∠FDE,所以DF∥AB,所以∠3=∠AEF.
因为∠3=∠B,所以∠B=∠AEF,所以FE∥BC,
所以∠AFE=∠ACB.
(2)因为∠1=80°,所以∠FDE=180°-∠1=100°.
因为∠3+∠FDE+∠FED=180°,
所以∠FED=180°-∠FDE-∠3=35°.
因为EF∥BC,所以∠BCE=∠FED=35°.
因为CE平分∠ACB,
所以∠ACB=2∠BCE=70°,
所以∠AFE=∠ACB=70°.

练习册系列答案
相关题目