题目内容
【题目】新定义:对于关于x的一次函数y=kx+b(k≠0),我们称函数y=![]() 为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
例如:对于关于x的一次函数y=x+4的3变函数为y=![]()
(1)关于x的一次函数y=-x+1的2变函数为![]() ,则当x=4时,
,则当x=4时,![]() = ;
= ;
(2)关于x的一次函数y=x+2的1变函数为![]() ,关于x的一次函数y=-
,关于x的一次函数y=-![]() x-2的-1变函数为
x-2的-1变函数为![]() ,求函数
,求函数![]() 和函数
和函数![]() 的交点坐标;
的交点坐标;
(3)关于x的一次函数y=2x+2的1变函数为![]() ,关于x的一次函数y=
,关于x的一次函数y=![]() x-1,的m变函数为
x-1,的m变函数为![]() .
.
①当-3≤x≤3时,函数![]() 的取值范围是 (直接写出答案):
的取值范围是 (直接写出答案):
②若函数![]() 和函数
和函数![]() 有且仅有两个交点,则m的取值范围是 (直接写出答案).
有且仅有两个交点,则m的取值范围是 (直接写出答案).
【答案】(1)3;(2) ![]() 和(0,2);(3) ①﹣8≤y1≤4; ②﹣2≤m<
和(0,2);(3) ①﹣8≤y1≤4; ②﹣2≤m<![]()
【解析】
(1)根据m变函数的定义即可解决问题;
(2)转化为方程组解决问题即可;
(3)①根据m变函数的定义,求出特殊点的函数值即可解决问题;
②利用方程组求出交点坐标即可解决问题;
(1)根据m变函数定义,关于x的一次函数y=﹣x+1的2变函数为:
![]() ,
,
∴x=4时,y=4﹣1=3,
故答案为3.
(2)根据定义得:y1:![]() ,y2:
,y2: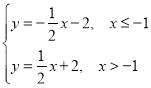 ,
,
则交点坐标有:
①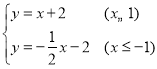 ,解得
,解得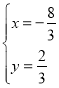 ;
;
②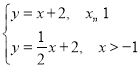 ,解得
,解得![]() ;
;
③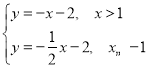 ,无解;
,无解;
④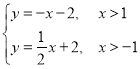 ,无解;
,无解;
综上所述函数y1和函数y2的交点坐标为![]() 和(0,2).
和(0,2).
(3)①由题意:y1:![]() ,
,
∴x=﹣3时,y=﹣4,x=3时,y=﹣8,
x=1时,y=4,
∴﹣8≤y1≤4
故答案为﹣8≤y1≤4.
②由题意:y1:![]() ,y2:
,y2: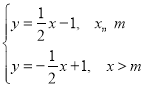 ,
,
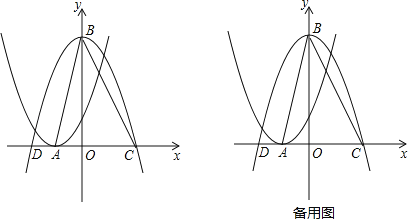
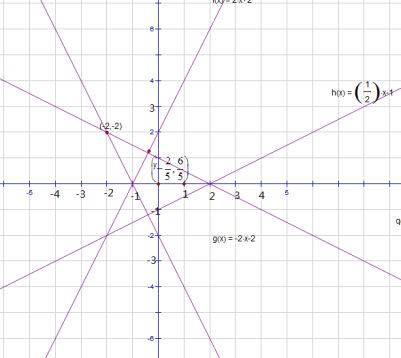
易知两个函数的交点(﹣2,﹣2),![]() ,
,
观察图象可知:﹣2≤m<![]() 时,函数y1和函数y2有且仅有两个交点.
时,函数y1和函数y2有且仅有两个交点.
故答案为:﹣2≤m<![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目