МвДҝДЪИЭ
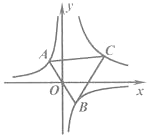
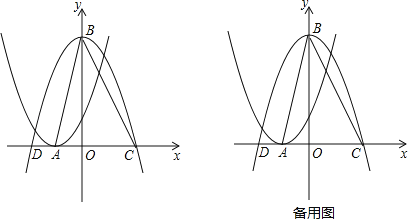
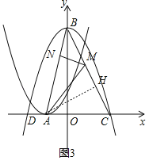
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬Ҫ«¶юҙОәҜКэy=x2+2x+1өДНјПуСШxЦб·ӯХЫЈ¬И»әуПтУТЖҪТЖ1ёцөҘО»Ј¬ФЩПтЙПЖҪТЖ4ёцөҘО»Ј¬өГөҪ¶юҙОәҜКэy=ax2+bx+cөДНјПуЈ®әҜКэy=x2+2x+1өДНјПуөД¶ҘөгОӘөгAЈ®әҜКэy=ax2+bx+cөДНјПуөД¶ҘөгОӘөгBЈ¬әНxЦбөДҪ»өгОӘөгCЈ¬DЈЁөгDО»УЪөгCөДЧуІаЈ©Ј®
ЈЁ1Ј©ЗуәҜКэy=ax2+bx+cөДҪвОцКҪЈ»
ЈЁ2Ј©ҙУөгAЈ¬CЈ¬DИэёцөгЦРИОИЎБҪёцөгәНөгB№№ФмИэҪЗРОЈ¬Зу№№ФмөДИэҪЗРОКЗөИСьИэҪЗРОөДёЕВКЈ»
ЈЁ3Ј©ИфөгMКЗПЯ¶ОBCЙПөД¶ҜөгЈ¬өгNКЗЎчABCИэұЯЙПөД¶ҜөгЈ¬КЗ·сҙжФЪТФAMОӘРұұЯөДRtЎчAMNЈ¬К№ЎчAMNөДГж»эОӘЎчABCГж»эөД![]() ЈҝИфҙжФЪЈ¬ЗуtanЎПMANөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
ЈҝИфҙжФЪЈ¬ЗуtanЎПMANөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©ҪвОцКҪОӘy=©Ғx2+4Ј»ЈЁ2Ј©№№ФмөДИэҪЗРОКЗөИСьИэҪЗРОөДёЕВККЗ![]() Ј»ЈЁ3Ј©ҙжФЪЈ¬tanЎПMANөДЦөОӘ1»т4»т
Ј»ЈЁ3Ј©ҙжФЪЈ¬tanЎПMANөДЦөОӘ1»т4»т![]() Ј®
Ј®
ЎҫҪвОцЎҝЈЁ1Ј©АыУГЕд·Ҫ·ЁөГөҪy=x2+2x+1=ЈЁx+1Ј©2Ј¬И»әуёщҫЭЕЧОпПЯөДұд»»№жВЙЗуҪвЈ»
ЈЁ2Ј©АыУГ¶ҘөгКҪy=ЈЁx+1Ј©2өГөҪAЈЁ©Ғ1Ј¬0Ј©Ј¬Ҫв·ҪіМ©Ғx2+4=0өГDЈЁ©Ғ2Ј¬0Ј©Ј¬CЈЁ2Ј¬0Ј©ТЧөГBЈЁ0Ј¬4Ј©Ј¬БРҫЩіцЛщУРөДИэҪЗРОЈ¬ФЩјЖЛгіцAC=3Ј¬AD=1Ј¬CD=4Ј¬AB=![]() Ј¬BC=2
Ј¬BC=2![]() Ј¬BD=2
Ј¬BD=2![]() Ј¬И»әуёщҫЭөИСьИэҪЗРОөДЕР¶Ё·Ҫ·ЁәНёЕВК№«КҪЗуҪвЈ»
Ј¬И»әуёщҫЭөИСьИэҪЗРОөДЕР¶Ё·Ҫ·ЁәНёЕВК№«КҪЗуҪвЈ»
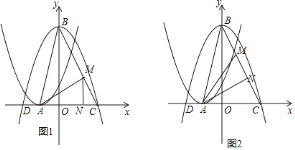
ЈЁ3Ј©ТЧөГBCөДҪвОцКЗОӘy=©Ғ2x+4Ј¬SЎчABC=6Ј¬MөгөДЧшұкОӘЈЁmЈ¬©Ғ2m+4Ј©ЈЁ0ЎЬmЎЬ2Ј©Ј¬МЦВЫЈәўЩөұNөгФЪACЙПЈ¬ИзНј1Ј¬АыУГГж»э№«КҪөГөҪ![]() ЈЁm+1Ј©ЈЁ©Ғ2m+4Ј©=2Ј¬ҪвөГm1=0Ј¬m2=1Ј¬өұm=0КұЈ¬ЗуіцAN=1Ј¬MN=4Ј¬ФЩАыУГХэЗР¶ЁТејЖЛгtanЎПMACөДЦөЈ»өұm=1КұЈ¬јЖЛгіцAN=2Ј¬MN=2Ј¬ФЩАыУГХэЗР¶ЁТејЖЛгtanЎПMACөДЦөЈ»ўЪөұNөгФЪBCЙПЈ¬ИзНј2Ј¬ПИАыУГГж»э·ЁјЖЛгіцAN=
ЈЁm+1Ј©ЈЁ©Ғ2m+4Ј©=2Ј¬ҪвөГm1=0Ј¬m2=1Ј¬өұm=0КұЈ¬ЗуіцAN=1Ј¬MN=4Ј¬ФЩАыУГХэЗР¶ЁТејЖЛгtanЎПMACөДЦөЈ»өұm=1КұЈ¬јЖЛгіцAN=2Ј¬MN=2Ј¬ФЩАыУГХэЗР¶ЁТејЖЛгtanЎПMACөДЦөЈ»ўЪөұNөгФЪBCЙПЈ¬ИзНј2Ј¬ПИАыУГГж»э·ЁјЖЛгіцAN=![]() Ј¬ФЩёщҫЭИэҪЗРОГж»э№«КҪјЖЛгіцMN=
Ј¬ФЩёщҫЭИэҪЗРОГж»э№«КҪјЖЛгіцMN=![]() Ј¬И»әуАыУГХэЗР¶ЁТејЖЛгtanЎПMACөДЦөЈ»ўЫөұNөгФЪABЙПЈ¬ИзНј3Ј¬ЧчAHЎНBCУЪHЈ¬ЙиAN=tЈ¬ФтBN=
Ј¬И»әуАыУГХэЗР¶ЁТејЖЛгtanЎПMACөДЦөЈ»ўЫөұNөгФЪABЙПЈ¬ИзНј3Ј¬ЧчAHЎНBCУЪHЈ¬ЙиAN=tЈ¬ФтBN=![]() ©ҒtЈ¬УЙўЪөГAH=
©ҒtЈ¬УЙўЪөГAH=![]() Ј¬АыУГ№ҙ№Й¶ЁАнҝЙјЖЛгіцBH=
Ј¬АыУГ№ҙ№Й¶ЁАнҝЙјЖЛгіцBH=![]() Ј¬ЦӨГчЎчBNMЎЧЎчBHAЈ¬АыУГПаЛЖұИҝЙөГөҪMN=
Ј¬ЦӨГчЎчBNMЎЧЎчBHAЈ¬АыУГПаЛЖұИҝЙөГөҪMN=![]() Ј¬АыУГИэҪЗРОГж»э№«КҪөГөҪ
Ј¬АыУГИэҪЗРОГж»э№«КҪөГөҪ![]() ЈЁ
ЈЁ![]() ©ҒtЈ©
©ҒtЈ©![]() =2Ј¬ёщҫЭҙЛ·ҪіМГ»УРКөКэҪвҝЙЕР¶ПөгNФЪABЙПІ»·ыәПМхјюЈ¬ҙУ¶шөГөҪtanЎПMANөДЦөОӘ1»т4»т
=2Ј¬ёщҫЭҙЛ·ҪіМГ»УРКөКэҪвҝЙЕР¶ПөгNФЪABЙПІ»·ыәПМхјюЈ¬ҙУ¶шөГөҪtanЎПMANөДЦөОӘ1»т4»т![]() Ј®
Ј®
ЈЁ1Ј©y=x2+2x+1=ЈЁx+1Ј©2өДНјПуСШxЦб·ӯХЫЈ¬өГy=©ҒЈЁx+1Ј©2Ј¬
°Сy=©ҒЈЁx+1Ј©2ПтУТЖҪТЖ1ёцөҘО»Ј¬ФЩПтЙПЖҪТЖ4ёцөҘО»Ј¬өГy=©Ғx2+4Ј¬
ЎаЛщЗуөДәҜКэy=ax2+bx+cөДҪвОцКҪОӘy=©Ғx2+4Ј»
ЈЁ2Ј©ЎЯy=x2+2x+1=ЈЁx+1Ј©2Ј¬
ЎаAЈЁ©Ғ1Ј¬0Ј©Ј¬
өұy=0КұЈ¬©Ғx2+4=0Ј¬ҪвөГx=ЎА2Ј¬ФтDЈЁ©Ғ2Ј¬0Ј©Ј¬CЈЁ2Ј¬0Ј©Ј»
өұx=0КұЈ¬y=©Ғx2+4=4Ј¬ФтBЈЁ0Ј¬4Ј©Ј¬
ҙУөгAЈ¬CЈ¬DИэёцөгЦРИОИЎБҪёцөгәНөгB№№ФмИэҪЗРОөДУРЈәЎчACBЈ¬ЎчADBЈ¬ЎчCDBЈ¬
ЎЯAC=3Ј¬AD=1Ј¬CD=4Ј¬AB=![]() Ј¬BC=2
Ј¬BC=2![]() Ј¬BD=2
Ј¬BD=2![]() Ј¬
Ј¬
ЎаЎчBCDОӘөИСьИэҪЗРОЈ¬
Ўа№№ФмөДИэҪЗРОКЗөИСьИэҪЗРОөДёЕВК=![]() Ј»
Ј»
ЈЁ3Ј©ҙжФЪЈ¬
ТЧөГBCөДҪвОцКЗОӘy=©Ғ2x+4Ј¬SЎчABC=![]() ACOB=
ACOB=![]() ЎБ3ЎБ4=6Ј¬
ЎБ3ЎБ4=6Ј¬
MөгөДЧшұкОӘЈЁmЈ¬©Ғ2m+4Ј©ЈЁ0ЎЬmЎЬ2Ј©Ј¬
ўЩөұNөгФЪACЙПЈ¬ИзНј1Ј¬
ЎаЎчAMNөДГж»эОӘЎчABCГж»эөД![]() Ј¬
Ј¬
Ўа![]() ЈЁm+1Ј©ЈЁ©Ғ2m+4Ј©=2Ј¬ҪвөГm1=0Ј¬m2=1Ј¬
ЈЁm+1Ј©ЈЁ©Ғ2m+4Ј©=2Ј¬ҪвөГm1=0Ј¬m2=1Ј¬
өұm=0КұЈ¬MөгөДЧшұкОӘЈЁ0Ј¬4Ј©Ј¬NЈЁ0Ј¬0Ј©Ј¬ФтAN=1Ј¬MN=4Ј¬
ЎаtanЎПMAC=![]() =4Ј»
=4Ј»
өұm=1КұЈ¬MөгөДЧшұкОӘЈЁ1Ј¬2Ј©Ј¬NЈЁ1Ј¬0Ј©Ј¬ФтAN=2Ј¬MN=2Ј¬
ЎаtanЎПMAC=![]() =1Ј»
=1Ј»
ўЪөұNөгФЪBCЙПЈ¬ИзНј2Ј¬
BC=![]() =2
=2![]() Ј¬
Ј¬
ЎЯ![]() BCAN=
BCAN=![]() ACBCЈ¬ҪвөГAN=
ACBCЈ¬ҪвөГAN=![]() Ј¬
Ј¬
ЎЯSЎчAMN=![]() ANMN=2Ј¬
ANMN=2Ј¬
ЎаMN=![]() =
=![]() Ј¬
Ј¬
ЎаЎПMAC=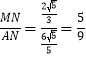 Ј»
Ј»
ўЫөұNөгФЪABЙПЈ¬ИзНј3Ј¬ЧчAHЎНBCУЪHЈ¬ЙиAN=tЈ¬ФтBN=![]() ©ҒtЈ¬
©ҒtЈ¬
УЙўЪөГAH=![]() Ј¬ФтBH=
Ј¬ФтBH=![]() Ј¬
Ј¬
ЎЯЎПNBG=ЎПHBAЈ¬
ЎаЎчBNMЎЧЎчBHAЈ¬
Ўа![]() Ј¬јҙ
Ј¬јҙ![]() Ј¬
Ј¬
ЎаMN=![]() Ј¬
Ј¬
ЎЯ![]() ANMN=2Ј¬
ANMN=2Ј¬
јҙ![]() ЈЁ
ЈЁ![]() ©ҒtЈ©
©ҒtЈ©![]() =2Ј¬
=2Ј¬
ХыАнөГ3t2©Ғ3![]() t+14=0Ј¬Ўч=ЈЁ©Ғ3
t+14=0Ј¬Ўч=ЈЁ©Ғ3![]() Ј©2©Ғ4ЎБ3ЎБ14=©Ғ15Јј0Ј¬·ҪіМГ»УРКөКэҪвЈ¬
Ј©2©Ғ4ЎБ3ЎБ14=©Ғ15Јј0Ј¬·ҪіМГ»УРКөКэҪвЈ¬
ЎаөгNФЪABЙПІ»·ыәПМхјюЈ¬
ЧЫЙПЛщКцЈ¬tanЎПMANөДЦөОӘ1»т4»т![]() Ј®
Ј®

 ұҰұҙјЖ»®ЖЪД©іеҙМ¶б100·ЦПөБРҙр°ё
ұҰұҙјЖ»®ЖЪД©іеҙМ¶б100·ЦПөБРҙр°ё ДЬҝјКФИ«ДЬ100·ЦПөБРҙр°ё
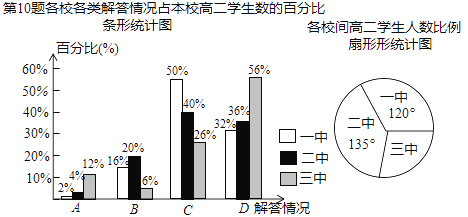
ДЬҝјКФИ«ДЬ100·ЦПөБРҙр°ёЎҫМвДҝЎҝЎ°К®Т»Ўұ»ЖҪрЦЬЖЪјдЈ¬ДіКРФЪ![]() МмЦРНвіцВГУОөДИЛКэұд»ҜИзПВұнЈЁХэКэұнКҫұИЗ°Т»Мм¶аөДИЛКэЈ¬ёәКэұнКҫұИЗ°Т»МмЙЩөДИЛКэЈ©
МмЦРНвіцВГУОөДИЛКэұд»ҜИзПВұнЈЁХэКэұнКҫұИЗ°Т»Мм¶аөДИЛКэЈ¬ёәКэұнКҫұИЗ°Т»МмЙЩөДИЛКэЈ©
ИХЖЪ |
|
|
|
|
|
|
|
ИЛКэұд»ҜЈЁНтИЛЈ© |
|
|
|
|
|
|
|
ЈЁ1Ј©Иф![]() ФВ
ФВ![]() ИХНвіцВГУОИЛКэОӘ
ИХНвіцВГУОИЛКэОӘ![]() Ј¬ДЗГҙ
Ј¬ДЗГҙ![]() ФВ
ФВ![]() ИХНвіцВГУОөДИЛКэКЗ¶аЙЩЈҝ
ИХНвіцВГУОөДИЛКэКЗ¶аЙЩЈҝ
ЈЁ2Ј©ЗлЕР¶ПЖЯМмДЪНвіцВГУОИЛКэЧо¶аөДКЗДДМмЈҝЧоЙЩөДКЗДДМмЈҝЛьГЗПаІо¶аЙЩЈҝ
ЈЁ3Ј©Из№ыЧо¶аТ»МмУРіцУОИЛКэ![]() НтИЛЈ¬ДЗГҙИф
НтИЛЈ¬ДЗГҙИф![]() ФВ
ФВ![]() ИХНвіцВГУОөДУР¶аЙЩИЛЈҝ
ИХНвіцВГУОөДУР¶аЙЩИЛЈҝ