题目内容
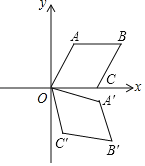
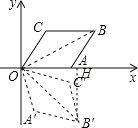
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
【答案】![]()
【解析】作B′H⊥x轴于H点,连结OB,OB′,根据菱形的性质得到∠AOB=30°,再根据旋转的性质得∠BOB′=75°,OB′=OB=2![]() ,则∠AOB′=∠BOB′﹣∠AOB=45°,所以△OBH为等腰直角三角形,根据等腰直角三角形性质可计算得OH=B′H=
,则∠AOB′=∠BOB′﹣∠AOB=45°,所以△OBH为等腰直角三角形,根据等腰直角三角形性质可计算得OH=B′H=![]() ,然后根据第四象限内点的坐标特征写出B′点的坐标.
,然后根据第四象限内点的坐标特征写出B′点的坐标.
作B′H⊥x轴于H点,连结OB,OB′,如图,
∵四边形OABC为菱形,
∴∠AOC=180°﹣∠C=60°,OB平分∠AOC,
∴∠AOB=30°,
∵菱形OABC绕原点O顺时针旋转75°至第四象限OA′B′C′的位置,
∴∠BOB′=75°,OB′=OB=2![]() ,
,
∴∠AOB′=∠BOB′﹣∠AOB=45°,
∴△OB′H为等腰直角三角形,
∴OH=B′H=![]() OB′=
OB′=![]() ,
,
∴点B′的坐标为(![]() ,﹣
,﹣![]() ),
),
故答案为:(![]() ,﹣
,﹣![]() ).
).

练习册系列答案
相关题目
【题目】“十一”黄金周期间,某市在![]() 天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
(1)若![]() 月
月![]() 日外出旅游人数为
日外出旅游人数为![]() ,那么
,那么![]() 月
月![]() 日外出旅游的人数是多少?
日外出旅游的人数是多少?
(2)请判断七天内外出旅游人数最多的是哪天?最少的是哪天?它们相差多少?
(3)如果最多一天有出游人数![]() 万人,那么若
万人,那么若![]() 月
月![]() 日外出旅游的有多少人?
日外出旅游的有多少人?