题目内容
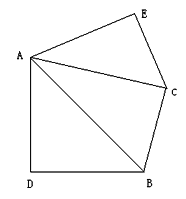
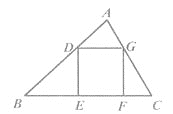
【题目】如图,△ABC中,正方形DEFG的顶点D,G分别在AB,AC上,顶点E,F在BC上.若△ADG、△BED、△CFG的面积分别是1、3、1,则正方形的边长为( )
A. ![]() B.
B. ![]() C. 2 D. 2
C. 2 D. 2![]()
【答案】C
【解析】
过点A作AM⊥BC于点M,AM交DG于点N,根据正方形的性质结合三角形的面积可得出AN=CF、BE=3CF,由DG∥EF可得出△ADG∽△ABC,根据相似三角形的性质可求出DG=2CF,再由△ADG的面积是1,即可求出DG的长度,此题得解.
过点A作AM⊥BC于点M,AM交DG于点N,如图所示.
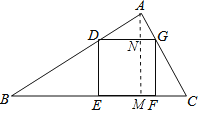
∵四边形DEFG为正方形,
∴DG∥EF,DG=DE=GF=EF.
根据题意得:![]() DGAN=1,
DGAN=1, ![]() DEBE=3,
DEBE=3,![]() GFCF=1,
GFCF=1,
∴AN=CF,BE=3CF.
∵DG∥EF,
∴△ADG∽△ABC,
∴![]() ,即
,即![]() ,
,
∴DG=2CF.
∵![]() DGAN=
DGAN=![]() ×
×![]() DGDG=1,
DGDG=1,
∴DG=2.
故选:C.

练习册系列答案
相关题目
【题目】“十一”黄金周期间,某市在![]() 天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
(1)若![]() 月
月![]() 日外出旅游人数为
日外出旅游人数为![]() ,那么
,那么![]() 月
月![]() 日外出旅游的人数是多少?
日外出旅游的人数是多少?
(2)请判断七天内外出旅游人数最多的是哪天?最少的是哪天?它们相差多少?
(3)如果最多一天有出游人数![]() 万人,那么若
万人,那么若![]() 月
月![]() 日外出旅游的有多少人?
日外出旅游的有多少人?