题目内容
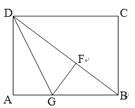
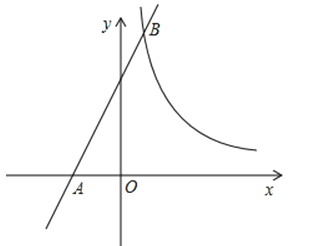
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(8,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求反比例函数的解析式和n的值;
(2)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求G点的坐标.
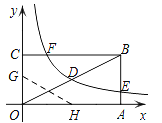
【答案】(1)反比例函数的解析式为![]() ,n=1;
,n=1;
(2)G点的坐标为(0,2.5)
【解析】解:(1)在Rt△BOA中 ∵OA=8 ,∴AB=OA×tan∠BOA=4
∵点D为OB的中点,点B(8,4),∴点D(4,2)
又∵点D在的图象上 , ∴![]()
∴k=8 ∴![]()
又∵点E在图象上 ∴8n=8 ∴ n=1
(2)设点F(a,4),∴4a=8 ,∴CF=a=2
连结FG,设OG=t,则OG=FG=t CG=4-t
Rt△CGF中,GF2=CF2+CG2
∴t2=(4-t)2+12 ,∴t=2.5,∴=2.5
∴G点的坐标为(0,2.5)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目