��Ŀ����
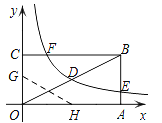
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��B��C������ֱ�Ϊ(-1��0)��(5��0)��(0��2)��
��1�����A��B��C����������߽���ʽ��
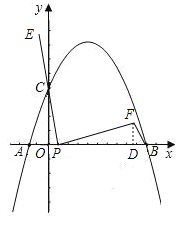
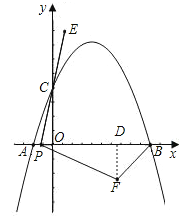
��2������P��A���������x����������ÿ��1����λ���ȵ��ٶ���B���ƶ�������PC���ӳ�����E��ʹCE=PC�����߶�PE�Ƶ�P˳ʱ����ת90��õ��߶�PF������FB������P�˶���ʱ��Ϊt��(0��t��6)�����PBF�����ΪS��
����S��t�ĺ�����ϵʽ��
�ڵ�t�Ƕ���ʱ����PBF���������������Ƕ��٣�
��3����P���ƶ��Ĺ����У���PBF�ܷ��Ϊֱ�������Σ����ܣ�ֱ��д����F�����ꣻ�����ܣ���˵�����ɣ�
���𰸡���1��![]() ;��2���� S��PBF=t2��7t+6��0��t��1��,S��PBF=��t2+7t��6��1��t��6������
;��2���� S��PBF=t2��7t+6��0��t��1��,S��PBF=��t2+7t��6��1��t��6������
��t=3.5ʱ�������������ֵΪ6.25;��3����,F������Ϊ����5�� ![]() ����5��2����
����5��2����
����������������1����Ϊ�����߹�A��B��C���㣬���Դ����������ʹ�����ߵĽ���ʽ��������2���ٴ���Ҫ������������������ۣ�
һ����P��λ��ԭ����࣬�߶�OA�ϣ���ʱ0��t<1������t��ʾ��OP��BP�ij��������BPF��������ؼ�Ҫ���BP���ϵĸߣ��ɹ�F��FD��x����D�����ڡ�CPF=90�㣬��֤����OPC�ס�DFP��������֪������֪PF=PE=2PC�����������������ε����Ʊ�Ϊ2����ôDF=2OP���ɴ˿ɵõ�DF�ij�����BPΪ�ף�DFΪ�ߣ�������á�BPF���������ʽ��Ҳ�͵õ��˹���S��t�ĺ�����ϵʽ��
������P��λ��ԭ���Ҳ࣬�߶�BP�ϣ���ʱ1<t<6���ɷ���һ�ķ���������⣻
�ڸ��ݢٵõ���S��t�ĺ�����ϵʽ������Ӧ���Ա�����ȡֵ��Χ�����ɸ��ݺ������������S�����ֵ����Ӧ��tֵ��Ȼ����бȽϼ��ɵõ������
��3����Pλ���߶�OA��ʱ����Ȼ��PFB��������ֱ�������Σ����ڡ�BPF<��CPF=90�㣬����P��������ֱ�Ƕ��㣬�ɷ���������������ۣ�
��FΪֱ�Ƕ��㣬��F��FD��x����D���ɣ�2����֪BP=6-t��DP=2OC=4����Rt��OCP�У�OP=t-1���ɹ��ɶ��������CP=t2-2t+5����ôPF=![]() =4��t-2t+5������Rt��PFB�У�FD��PB������Ӱ���������PB=PF��PD=t-2t+5����PB����һ������ʽΪ��PB=6-t��������ʽ�ɵ�t-2t+5=6-t����t=
=4��t-2t+5������Rt��PFB�У�FD��PB������Ӱ���������PB=PF��PD=t-2t+5����PB����һ������ʽΪ��PB=6-t��������ʽ�ɵ�t-2t+5=6-t����t=![]() ��
��
��BΪֱ�Ƕ��㣬��ô��ʱ������루2�������ƣ���PFB�ס�CPO�������Ʊ�Ϊ2����ôBP=2OC=4����OP=OB-BP=1����ʱt=2��
�����������1������һ���������ߵĽ���ʽΪy=ax2+bx+c��a��0����
��A����1��0����B��5��0����C��0��2��
����������ʽ�ã� 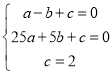 �� ���
�� ���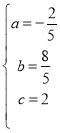
��![]() ��
��
���������������ߵĽ���ʽΪy=a��x��5����x+1����
�ѣ�0��2���������ʽ�ã�2=��5a��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��2���ٹ���F��FD��x����D��
����P��ԭ�����ʱ��BP=6��t��OP=1��t��
��Rt��POC�У���PCO+��CPO=90�㣬
���FPD+��CPO=90�㣬
�ߡ�PCO=��FPD��
���POC=��FDP��
���CPO�ס�PFD��
��![]()
��PF=PE=2PC��
��FD=2PO=2��1��t����
��S��PBF= ![]() =t2��7t+6��0��t��1����
=t2��7t+6��0��t��1����
����P��ԭ���Ҳ�ʱ��OP=t��1��BP=6��t��
�ߡ�CPO�ס�PFD��
��FD=2��t��1������S��PBF= ![]() =��t2+7t��6��1��t��6����
=��t2+7t��6��1��t��6����
�ڵ�0��t��1ʱ��S=t2��7t+6��
��ʱt��t=3.5����࣬S��t���������С��
���У���t=0ʱ��Smax=0��7��0+6=6��
��1��t��6ʱ��S=��t2+7t��6��
����1��3.5��6���ʵ�t=3.5ʱ��Smax=��3.5��3.5+7��3.5+6=6.25��
������������t=3.5ʱ�������������ֵΪ6.25��
��3���ܣ�����FΪֱ�Ƕ��㣬��F��FD��x����D��
�ɣ�2����֪BP=6��t��DP=2OC=4��
��Rt��OCP��OP=t��1��
�ɹ��ɶ��������CP2=t2��2t+5��
��ôPF
��Rt��PFB��FD��PB��
����Ӱ���������PB=PF2��PD=t2��2t+5��
��PB����һ������ʽΪ��PB=6��t��
������ʽ�ɵ�t2��2t+5=6��t��
��t=![]() ��P��������
��P��������![]() ��0����
��0����
��F����������5�� ![]() ����
����
��BΪֱ�Ƕ��㣬��ô��ʱ������루2�������ƣ���PFB�ס�CPO�������Ʊ�Ϊ2��
��ôBP=2OC=4����OP=OB��BP=1����ʱt=2��P������Ϊ��1��0����FD=2��t��1��=2��
��F��������5��2����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�