题目内容
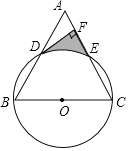
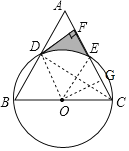
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
【答案】(1)证明见解析;(2)![]()
【解析】(1)连接CD、OD,先利用等腰三角形的性质证AD=BD,再证OD为△ABC的中位线得DO∥AC,根据DF⊥AC可得;
(2)连接OE、作OG⊥AC,求出EF、DF的长及∠DOE的度数,根据阴影部分面积=S梯形EFDO-S扇形DOE计算可得.
(1)如图,连接CD、OD,
∵BC是⊙O的直径,
∴∠CDB=90°,即CD⊥AB,
又∵△ABC是等边三角形,
∴AD=BD,
∵BO=CO,
∴DO是△ABC的中位线,
∴OD∥AC,
∵DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE、作OG⊥AC于点G,
∴∠OGF=∠DFG=∠ODF=90°,
∴四边形OGFD是矩形,
∴FG=OD=4,
∵OC=OE=OD=OB,且∠COE=∠B=60°,
∴△OBD和△OCE均为等边三角形,
∴∠BOD=∠COE=60°,CE=OC=4,
∴EG=![]() CE=2、DF=OG=OCsin60°=2
CE=2、DF=OG=OCsin60°=2![]() ,∠DOE=60°,
,∠DOE=60°,
∴EF=FG-EG=2,
则阴影部分面积为S梯形EFDO-S扇形DOE
=![]() ×(2+4)×2
×(2+4)×2![]() -
-![]()
=![]() .
.

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目