题目内容
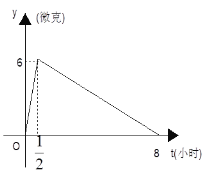
【题目】某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如图所示曲线:
(1)分别求出![]() 和
和![]() 时,y与t之间的函数关系式;
时,y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为7:00,那么服药后几点到几点有效?
【答案】(1) 当![]() 时,y1=12t; 当t≥
时,y1=12t; 当t≥![]() 时,
时,![]() ;(2) 7:20到10:00有效.
;(2) 7:20到10:00有效.
【解析】
(1)当![]() 时,y与t成正比例函数,
时,y与t成正比例函数,![]() 时,y与t是一次函数关系,利用待定系数法求解即可.
时,y与t是一次函数关系,利用待定系数法求解即可.
(2)利用函数的性质把y=4分别代入两函数的解析式即可求出答案.
解:(1)当![]() 时,设y1=kt,图象经过点(
时,设y1=kt,图象经过点(![]() ,6),
,6),
代入解得:k=12,所以y1=12t.
当t≥![]() 时,设y2=kt+b,图象经过点(
时,设y2=kt+b,图象经过点(![]() ,6)和点(8,0).
,6)和点(8,0).
代入列出方程组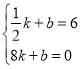
解得:![]() ,所以
,所以![]() .
.
(2)解:∵每毫升血液中含药量不少于4微克时治疗疾病有效,
∴把y=4代入y1=12t得:4=12t,
解得:t=![]() ,
,
即![]() 小时=20分钟;7点再过20分钟是7:20;
小时=20分钟;7点再过20分钟是7:20;
把y=4代入![]() 得:
得:![]() ,
,
解得:t=3,7:00再过三个小时也就是10:00.
即每毫升血液中含药量不少于4微克时是在服药后![]() 小时到3小时内有效,即从7:20到10:00有效.
小时到3小时内有效,即从7:20到10:00有效.

练习册系列答案
相关题目