题目内容
【题目】如图,牧童在A处放牛,其家在C处,A、C到河岸L的距离分别为AB=2km,CD=4km且,BD=8km。
(1)牧童从A处将牛牵到河边P处饮水后再回到家C,试确定P在何处,所走路程最短?请在图中画出饮水的位置(保留作图痕迹),不必说明理由。
(2)求出(1)中的最短路程。

【答案】(1)见解析;(2)10km.
【解析】试题分析:(1)作点A关于直线l的对称点A′,连接A′C交l于点P,则P点即为所求点;
(2)过A′作A′E⊥CD,交CD的延长线于E,再根据勾股定理即可得出A′C的长.
试题解析:
(1)如图:
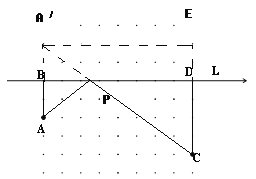
(2)由作图可得最短路程为A′C的距离,
过A′作A′E⊥CD,交CD的延长线于E,
则DE=A′B=AB=2km,A′E=BD=8km,CE=2+4=6km,
根据勾股定理可得,A′C=10km.

练习册系列答案
相关题目