Question

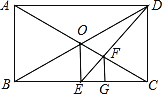
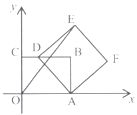
【题目】如图，在平面直角坐标系中，已知矩形OABC的顶点A在x轴上，OA=4，OC=3，点D为BC边上一点，以AD为一边在与点B的同侧作正方形ADEF，连接OE。当点D在边BC上运动时，OE的长度的最小值是________

Answer 1

【答案】5

【解析】

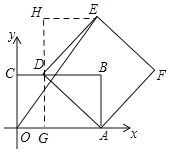
过点D作DG⊥OA，过点E作HE⊥DG．先证明△HED≌△GDA，从而得到HE=DG=3，HD=AG．设D（a，3），则DC=a，DH=AG=4-a，则E（a+3，7-a），依据两点间的距离公式可得到OE=，最后利用配方法求得被开方数的最小值即可．

如图所示：过点D作DG⊥OA，过点E作HE⊥DG．

∵DG⊥OA，HE⊥DG，

∴∠EHD=∠DGA=90°．

∴∠GDA+∠DAG=90°．

∵四边形ADEF为正方形，

∴DE=AD，∠HDE+∠GDA=90°．

∴∠HDE=∠GAD．

在△HED和△GDA中

，

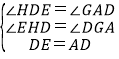∴△HED≌△GDA．

∴HE=DG=3，HD=AG．

设D（a，3），则DC=a，DH=AG=4-a．

∴E（a+3，7-a）．

∴OE==．

当a=2时，OE有最小值，最小值为5．