Question

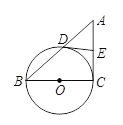
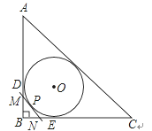
【题目】如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D、E，过劣弧DE（不包括端点D，E）上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为4cm，则Rt△MBN的周长为________cm.

Answer 1

【答案】8

【解析】

连接OD、OE，由切线性质易得四边形ODBE为正方形.由切线长定理可知MD=MP，NP=NE，则Rt△MBN的周长等于BD+BE.

解：连接OD、OE，

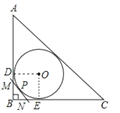
由切线性质可知OD⊥AB、OE⊥BC，再结合∠B=90°且OD=OE可知四边形ODBE为正方形，则BD=BE=OE=4cm.由切线长定理可知MD=MP，NP=NE，则：

Rt△MBN的周长=BM+MN+BN=BM+MD+BN+NE=BD+BE=4+4=8cm，

故答案为：4cm.