题目内容
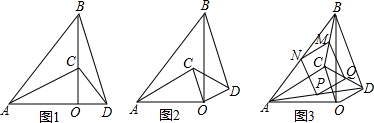
两块大小不同的含45°角的三角板AOB和三角板COD,直角顶点重合,三角板的两直角边重合(如图1)
(1)连结AC、BD,则AC和BD的①数量关系是AC BD;②位置关系是AC BD(直接写出结果,不必证明);
(2)将三角板COD绕点O顺时针旋转角度α(0°<α<360°),如图2,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)如图3,在(2)中,若M、N、P、Q分别是线段CB、AB、AD、CD的中点,请判断四边形MNPQ的形状,并给出证明.
(1)连结AC、BD,则AC和BD的①数量关系是AC
(2)将三角板COD绕点O顺时针旋转角度α(0°<α<360°),如图2,(1)中的结论是否成立?若成立,写出证明过程;若不成立,请说明理由;
(3)如图3,在(2)中,若M、N、P、Q分别是线段CB、AB、AD、CD的中点,请判断四边形MNPQ的形状,并给出证明.

考点:全等三角形的判定与性质,三角形中位线定理,正方形的判定
专题:
分析:(1)AC=BD,AC⊥BD.通过全等三角形△AOC≌△BOD的对应边相等证得AC=BD;如图1,延长AC交BD于点E,则∠AOB=∠AEB=90°;
(2)证法同(1);
(3)由三角形中位线定理和平行四边形的判定定理易证四边形MNPQ为平行四边形;然后利用AC=BD,AC⊥BD得到MN=MQ,且MN⊥MQ,故平行四边形MNPQ是正方形.
(2)证法同(1);
(3)由三角形中位线定理和平行四边形的判定定理易证四边形MNPQ为平行四边形;然后利用AC=BD,AC⊥BD得到MN=MQ,且MN⊥MQ,故平行四边形MNPQ是正方形.
解答: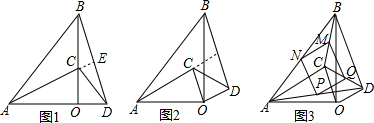 AC解:(1)①AC=BD.理由如下:
AC解:(1)①AC=BD.理由如下:
如图1,
在△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
②AC⊥BD.理由如下:
如图1,延长AC交BD于点E.
由①知,△AOC≌△BOD,
∴∠CAO=DBO.
又∵∠CAO+∠ACO=90°,∠BCE=∠ACO,
∴∠DBO+∠BCE=90°,
∴∠AEB=90°,即AC⊥BD;
故填:=;⊥;
(2)(1)中的结论都仍然成立.理由如下:
如图2,∵∠AOB=∠COD=90°,
∴∠AOB-∠BOC=∠COD-∠BOC,即∠AOC=∠BOD,
在△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
如图2,延长AC交BD于点E.
由①知,△AOC≌△BOD,
∴∠CAO=DBO.
又∵∠CAO+∠ACO=90°,∠BCE=∠ACO,
∴∠DBO+∠BCE=90°,
∴∠AEB=90°,即AC⊥BD.
综上所述,AC=BD,AC⊥BD;
(3)四边形MNPQ是正方形.证明如下:
∵如图3,M、N、P、Q分别是线段CB、AB、AD、CD的中点,
∴MN
AC,PQ
AC,
∴MN
PQ,
∴四边形MNPQ为平行四边形,
同理,MQ
BD.
又∵AC=BD,AC⊥BD,
∴MN=MQ,且MN⊥MQ,
∴平行四边形MNPQ为正方形,即四边形MNPQ是正方形.
 AC解:(1)①AC=BD.理由如下:
AC解:(1)①AC=BD.理由如下:如图1,
在△AOC与△BOD中,
|
∴△AOC≌△BOD(SAS),
∴AC=BD;
②AC⊥BD.理由如下:
如图1,延长AC交BD于点E.
由①知,△AOC≌△BOD,
∴∠CAO=DBO.
又∵∠CAO+∠ACO=90°,∠BCE=∠ACO,
∴∠DBO+∠BCE=90°,
∴∠AEB=90°,即AC⊥BD;
故填:=;⊥;
(2)(1)中的结论都仍然成立.理由如下:
如图2,∵∠AOB=∠COD=90°,
∴∠AOB-∠BOC=∠COD-∠BOC,即∠AOC=∠BOD,
在△AOC与△BOD中,
|
∴△AOC≌△BOD(SAS),
∴AC=BD;
如图2,延长AC交BD于点E.
由①知,△AOC≌△BOD,
∴∠CAO=DBO.
又∵∠CAO+∠ACO=90°,∠BCE=∠ACO,
∴∠DBO+∠BCE=90°,
∴∠AEB=90°,即AC⊥BD.
综上所述,AC=BD,AC⊥BD;
(3)四边形MNPQ是正方形.证明如下:
∵如图3,M、N、P、Q分别是线段CB、AB、AD、CD的中点,
∴MN
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴MN
| ∥ |
. |
∴四边形MNPQ为平行四边形,
同理,MQ
| ∥ |
. |
又∵AC=BD,AC⊥BD,
∴MN=MQ,且MN⊥MQ,
∴平行四边形MNPQ为正方形,即四边形MNPQ是正方形.
点评:本题综合考查了三角形中位线定理、全等三角形的判定与性质以及正方形的判定.正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个矩形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个矩形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若an+1•an-2=a5,且a≠1,则n等于( )
| A、3 | B、4 | C、5 | D、6 |
 如图,在?ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.
如图,在?ABDC中,分别取AC、BD的中点E和F,连接BE、CF,过点A作AP∥BC,交DC的延长线于点P.