题目内容

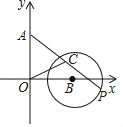
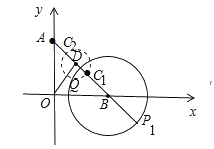
【题目】如图，在平面直角坐标系中，A（0，3）、B（3，0），以点B为圆心、2为半径的⊙B上有一动点P．连接AP，若点C为AP的中点，连接OC，则OC的最小值为（　　）

A. 1 B. 2﹣1 C. D. ﹣1

【答案】D

【解析】

确定点C的运动路径是:以D为圆心,以为半径的圆,当O、C、D共线时,OC的长最小,先求D的半径为1,说明D是AB的中点,根据直角三角形斜边中线是斜边一半可得OD=,所以OC的最小值是.

当点P运动到AB的延长线上时,即如图中点, 是的中点，

当点P在线段AB上时,是中点,取的中点为D，
点C的运动路径是以D为圆心,以D为半径的圆(CA:PA=1:2,则点C轨迹和点P轨迹相似,所以点C的轨迹就是圆),当O、C、D共线时,OC的长最小，设线段AB交B于Q，

中，OA=3,OB=3,

.

半径为2,

是的中点,

是的中点,

/p>

即半径为1,

故选D.

练习册系列答案
相关题目

【题目】（6分）如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．

（1）请画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标；

（2）请画出△ABC绕点B逆时针旋转90°后的△A2BC2；

（3）求出（2）中C点旋转到C2点所经过的路径长（记过保留根号和π）．

【题目】如图，在△ABC中，∠ABC＝90°，AB＝BC＝2，∠BAC，∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，则EF的长为_____．

【题目】解方程：

（1）(2x-1)2-25=0 （2） （3）

【题目】在△ABC中，AD是它的角平分线．

（1）如图1，求证：S△ABD：S△ACD＝AB：AC＝BD：CD；

（2）如图2，E是AB上的点，连接ED，若BD＝3，BE＝CD＝2，AE＝2CD，求证：△BED是等腰三角形；

（3）在图1中，若3∠BAC＝2∠C，∠ADB＞∠B＞∠BAD，直接写出∠BAC的取值范围　 　．

【题目】现有长度分别为3cm、4cm、5cm、8cm的4根木条

（1）李鑫同学从中任取一根，抽到“长度是4cm的木条”的概率是　　．

（2）在李鑫同学取出4cm的木条后，王华同学又从剩下的木条中，同时随机取出两根，求他们取出的三根木条能构成三角形的概率．

【题目】如图，△ABC和△CDE都是等边三角形，B，C，D三点在一条直线上，AD与BE交于点P，AC，BE交于点M，AD，CE交于点N，连接MN，则下列五个结论：①AD=BE；②∠BMC=∠ANE；③∠APM=60°；④AN=BM；⑤△CMN是等边三角形．其中一定正确的是__________．（填出所有正确结论的序号）

【题目】如图，O是等边△ABC内一点，OA=3，OB=4，OC=5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：

①△BO′A可以由△BOC绕点B逆时针旋转60°得到；&

②点O与O′的距离为4；

③∠AOB=150°；

④四边形AOBO′的面积为6＋3 ；

⑤S△AOC＋S△AOB=6＋.

其中正确的结论是_______________．

【题目】如图，在平行四边形ABCD中，AC，BD相交于点O，AC＝6，BD＝8，∠AOD＝65°，点E在BO上，AF∥CE交BD于点F．

（1）求证：四边形AFCE是平行四边形．

（2）当点E在边BO上移动时，平行四边形AFCE能否为矩形？若能，此时BE的长为多少（直接写出结果）？若不能，请说明理由．

（3）当点E在边BO上移动时，平行四边形AFCE能否为菱形？若能，此时BE的长为多少（直接写出结果）？若不能，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网