Question

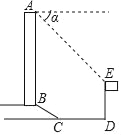
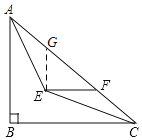
【题目】如图，在△ABC中，∠ABC＝90°，AB＝BC＝2，∠BAC，∠ACB的平分线相交于点E，过点E作EF∥BC交AC于点F，则EF的长为_____．

Answer 1

【答案】2﹣

【解析】

过E作EG∥AB，交AC于G，易得AG＝EG，EF＝CF，依据△ABC∽△GEF，即可得到EG：EF：GF＝1：1：，故设EG＝k＝AG，则EF＝k＝CF，FG＝k，根据AC＝2，可得k+k+k＝，于是得到结论．

解：如图，过E作EG∥AB，交AC于G，则∠BAE＝∠AEG，

∵AE平分∠BAC，

∴∠BAE＝∠CAE，

∴∠CAE＝∠AEG，

∴AG＝EG，

同理可得，EF＝CF，

∵AB∥GE，BC∥EF，

∴∠BAC＝∠EGF，∠BCA＝∠EFG，

∴△ABC∽△GEF，

∵∠ABC＝90°，AB＝BC＝2，

∴AC＝2，

∴EG：EF：GF＝AB：BC：AC＝1：1：，

设EG＝k＝AG，则EF＝k＝CF，FG＝k，

∵AC＝2，

∴k+k+k＝2，

∴k＝（2﹣），

∴EF＝k＝2﹣．

故答案为：2﹣