Question

【题目】如图，已知点A的坐标为（ ，3），AB丄x轴，垂足为B，连接OA，反比例函数y= （k＞0）的图象与线段OA、AB分别交于点C、D．若AB=3BD，以点C为圆心，CA的 倍的长为半径作圆，则该圆与x轴的位置关系是（填”相离”，“相切”或“相交“）．

Answer 1

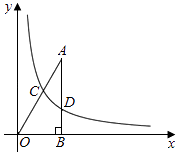
【答案】相交
【解析】解：∵已知点A的坐标为（ ，3），AB=3BD， ∴AB=3，BD=1，
∴D点的坐标为（ ，1），
∴反比例函数y= 解析式为：
y= ，
∴AO直线解析式为：y=kx，
3= k，
∴k= ，
∴y= x，
∴直线y= x与反比例函数y= 的交点坐标为：
x=±1，
∴C点的横坐标为1，
纵坐标为： ，
过C点做CE垂直于OB于点E，
则CO=2，
∴AC=2 ﹣2，
∴CA的 倍= ，
CE= ，
∵ ﹣ = ﹣ ＞0，
∴该圆与x轴的位置关系是相交．
所以答案是：相交．

【考点精析】本题主要考查了直线与圆的三种位置关系的相关知识点，需要掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点才能正确解答此题．