题目内容
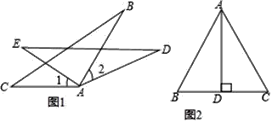
【题目】已知在△ABC中,∠BAC=90°,过点C的直线EF∥AB,D是BC上一点,连接AD,过点D分别作GD⊥AD,HD⊥BC,交EF和AC于点G,H,连接AG.
(1)当∠ACB=30°时,如图1所示.
①求证:△GCD∽△AHD;
②试判断AD与DG之间的数量关系,并说明理由;
(2)当tan∠ACB= ![]() 时,如图2所示,请你直接写出AD与DG之间的数量关系.
时,如图2所示,请你直接写出AD与DG之间的数量关系.
【答案】
(1)
①证明:∵∠BAC=90°,EF∥AB,
∴∠GCM=∠BAC=90°,
∵GD⊥AD,
∴∠ADM=90°,
∴∠GCA=∠ADM,
∵∠AND=∠GMC,
∴DAH=∠∠CGD,
∵∠ADH=∠CDG=90°﹣∠HDG
∴△GCD∽△AHD;
②解:由①知:△GCD∽△AHD,
∴ ![]() ,
,
在Rt△DHC中,
∵∠ACB=30°,
![]() =tan30°=
=tan30°= ![]() ,
,
∴ ![]() =
= ![]() ;
;
(2)
5AD=4DG,
解:由①知△GCD∽△AHD,
在Rt△DHC中,
∵tan∠ACB= ![]() ,
,
∴ ![]() =
= ![]() .
.
【解析】(1)①根据平行线的性质得到∠GCM=∠BAC=90°,根据垂直的定义得到∠ADM=90°,于是求得∠GCA=∠ADM,推出∠DAH=∠∠CGD,根据相似三角形的判定定理即可得到结论;②根据相似三角形的性质得到 ![]() ,根据三角函数的定义即可得到结论;(2)根据相似三角形的性质得到
,根据三角函数的定义即可得到结论;(2)根据相似三角形的性质得到 ![]() ,根据tan∠ACB=
,根据tan∠ACB= ![]() ,即可得到结论.
,即可得到结论.
【考点精析】掌握相似图形和相似三角形的性质是解答本题的根本,需要知道形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例;对应角相等,对应边成比例的两个三角形叫做相似三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目