Question

【题目】如图1，在△ABC中，∠ACB=90°，AC=BC，CD为AB边上的中线，点E、F分别在AC、BC边上，且ED⊥DF.

(1)求证：△CDE≌△BDF；

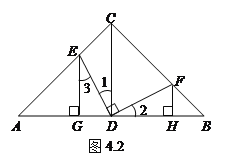
(2)如图2，作EG⊥AB于G，FH⊥AB于H，求证：EG+FH=CD．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】

试题

（1）由已知条件易证CD=BD，∠CDE=∠BDF，∠DCE=∠B=45°，从而可得△CDE≌△BDF；

（2）由（1）中所证△CDE≌△BDF可得DE=DF，由已知条件易证∠EGD=∠DHF=90°，∠DEG=∠FDH，由此可证得△DEG≌△FDH，从而可得：EG=DH；再证△BFH是等腰直角三角形得到FH=BH，即可得到所求结论.

试题解析：

（1）∵ 在△ABC中，∠ACB=90°，AC=BC，CD为AB上的中线，

∴ CD=BD，∠DCE=∠B=45°，∠CDB=90°.

∵ ED⊥DF，

∴ ∠EDF=90°，

∴ ∠CDE+∠CDF=∠BDF+∠CDF=90°

∴ ∠CDE=∠BDF.

∴ △CDE≌△BDF（ASA）.

（2）如图4.2，由（1）知，△CDE≌△BDF，

∴ DE=DF，∠1=∠2.

∵ EG⊥AB，FH⊥AB，CD⊥AB，∠B=45°，

∴∠EGD=∠DHF=∠BHF=90°, EG∥CD，

∴ ∠1=∠3，△BFH为等腰直角三角形，

∴ ∠3=∠2，FH=BH，

∴ △DEG≌△FDH（AAS）.

∴ EG=DH.

∴ EG+FH=DH+FH=DH+BH=BD.

∵ 由（1）可知BD=CD，

∴ EG+FH=CD.