题目内容
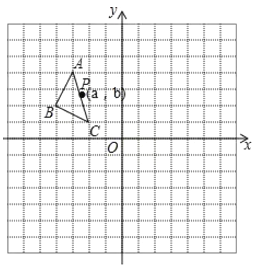
【题目】如图,在平面直角坐标系中,![]() 为
为![]() 的对称中心,
的对称中心,![]() ,
,![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 的坐标点为
的坐标点为![]() ,反比例函数
,反比例函数![]() 的图像经过点
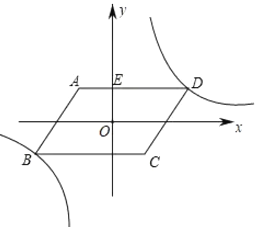
的图像经过点![]() .将
.将![]() 沿
沿![]() 轴向上平移,使点
轴向上平移,使点![]() 的对应点
的对应点![]() 落在反比例函数的图像上,则平移过程中线段
落在反比例函数的图像上,则平移过程中线段![]() 扫过的面积为( )
扫过的面积为( )
A.6B.8C.24D.![]()
【答案】D
【解析】
根据O为ABCD的对称中心,AD=5,AD∥x轴交y轴于点E,点A的坐标为(-2,2),可求点C、D的坐标,进而求出反比例函数的关系式,由平移可求出点![]() 的坐标,知道平移的距离,即平行四边形的底,再根据面积公式求出结果.
的坐标,知道平移的距离,即平行四边形的底,再根据面积公式求出结果.
解:∵AD=5,AD∥x轴交y轴于点E,点A的坐标为(-2,2),
∴DE=5-2=3,OE=2,
∴D(3,2),
把![]() 代入反比例函数的关系式得,k=2×3=6,
代入反比例函数的关系式得,k=2×3=6,
∵O为ABCD的对称中心,点A的坐标为(-2,2),
∴点C的坐标为(2,-2), 当x=2时,y=![]() ,
,
∴点![]() (2,3)
(2,3)
∴C![]() =CF+F
=CF+F![]() =2+3=5,
=2+3=5,
![]() 上的高是是
上的高是是![]()
∴平行四边形AC![]() N的面积为
N的面积为![]()
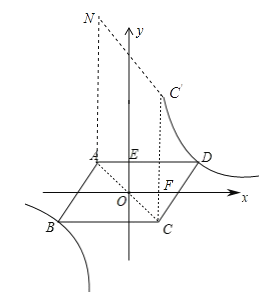
![]() 平移过程中线段
平移过程中线段![]() 扫过的面积为
扫过的面积为![]()
故选:D.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案【题目】下表是小安填写的数学实践活动报告的部分内容
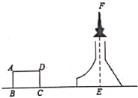
题 目 | 测量铁塔顶端到地面的高度 | |
测量目标示意图 |
|
|
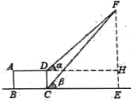
相关数据 | CD=20m,ɑ=45°,β=52° | |
求铁塔的高度FE(结果精确到1米)(参考数据:sin52°≈0.79, cos52°≈0.62,tan52°≈1.28)
【题目】某校为调查“停课不停学”期间九年级学生平均每天上网课时长,随机抽取了![]() 名九年级学生做网络问卷调查.共四个选项:
名九年级学生做网络问卷调查.共四个选项:![]() 小时以下)、
小时以下)、![]() 小时)、
小时)、![]() 小时),
小时), ![]() 小时以上),每人只能选一
小时以上),每人只能选一
项.并将调查结果绘制成如下不完整的统计表和统计图.
被调查学生平均每天上网课时间统计表
时长 | 所占百分比 |
|
|
|
|
|
|
|
|
合计 |
|
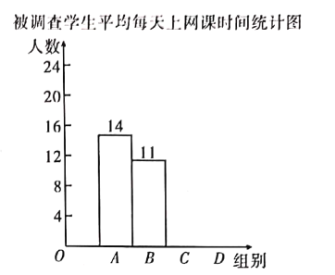
根据以上信息,解答下列问题:
![]() ,
,![]() ,
,
![]() 补全条形统计图;
补全条形统计图;
![]() 该校有九年级学生
该校有九年级学生![]() 名,请你估计仝校九年级学生平均每天上网课时长在
名,请你估计仝校九年级学生平均每天上网课时长在![]() 小时及以上的共多少名;
小时及以上的共多少名;
![]() 在被调查的对象中,平均每天观看时长超过
在被调查的对象中,平均每天观看时长超过![]() 小时的,有
小时的,有![]() 名来自九
名来自九![]() 班,
班,![]() 名来自九
名来自九![]() 班,其余都来自九
班,其余都来自九![]() 班,现教导处准备从
班,现教导处准备从![]() 选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的
选项中任选两名学生进行电话访谈,请用列表法或画树状图的方法求所抽取的![]() 名学生恰好来自同一个班级的概率.
名学生恰好来自同一个班级的概率.