Question

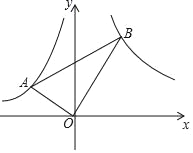
【题目】如图，已知A是函数y=﹣ （x＜0）图象上一点，B是函数y= （x＞0）图象上一点，若OA⊥OB且AB=2，则点A的横坐标为______．

Answer 1

【答案】﹣2或﹣1．

【解析】

作AE⊥x轴于E，BF⊥x轴于F．设A（a，﹣），B（b，），则a＜0，b＞0．根据题意可知△BOF∽△OAE，所以，得a2b2=12，根据勾股定理 可知AB2=OB2+OA2=b2++a2+，整理得b2=15﹣3a2，根据a2b2=12得a2（15﹣3a2）=12，求出a的值即可.

如图，作AE⊥x轴于E，BF⊥x轴于F．设A（a，﹣），B（b，），则a＜0，b＞0．

∵∠AOB=∠OFB=∠AEO=90°，

∴∠BOF+∠AOE=90°，∠AOE+∠OAE=90°，

∴∠BOF=∠OAE，

∴△BOF∽△OAE，

∴

∴

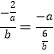
∴a2b2=12，

∵AB2=OB2+OA2=b2++a2+，AB=2，

∴b2++a2+=20，

两边同乘a2b2，得12（b2+a2）+36a2+4b2=20×12，

化简整理，得b2=15﹣3a2，

∵a2b2=12，

∴a2（15﹣3a2）=12，

解得a=±1或±2，

∵a＜0，

∴a=﹣2或﹣1．

故答案为﹣2或﹣1