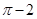题目内容
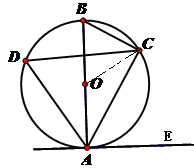
如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.
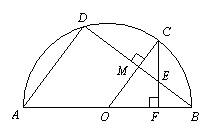
(1)求⊙O的半径;
(2)求证:CE=BE.

(1)求⊙O的半径;
(2)求证:CE=BE.
(1)5;(2)证明见解析.
试题分析:(1)可在Rt△OBM中,用半径表示出OM,然后根据勾股定理求出半径的长;(2)由AAS证得
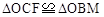 ,由等量减等量差相等得
,由等量减等量差相等得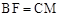 ,从而由AAS或ASA可证得
,从而由AAS或ASA可证得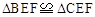 ,因此CE = BE
,因此CE = BE试题解析:(1)∵AB为直径,∴
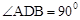 .
.∵OC⊥BD,∴M为BD的中点.
∵BD=8,∴
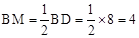 .
.设半径为r,则OM=OC-CM=r-2,
∴在
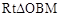 中,
中,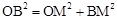 ,即
,即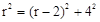 ,解得
,解得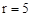 .
.∴⊙O的半径为5.
(2)在
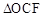 和
和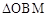 中,∵∠COF=∠BOM(公共角),∠CFO=∠BMO=90°,OC=OM1
中,∵∠COF=∠BOM(公共角),∠CFO=∠BMO=90°,OC=OM1∴
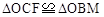 (AAS), ∴OF=OM.
(AAS), ∴OF=OM.又OB=OC,∴
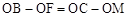 ,即
,即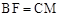 .
.∴
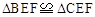 (AAS或ASA). ∴CE = BE.
(AAS或ASA). ∴CE = BE.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
.
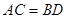
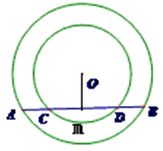
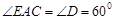 .
.
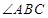 的度数;
的度数;