题目内容
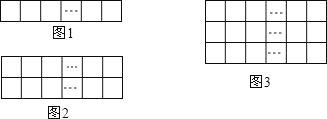
【题目】.现有 a 根长度相同的火柴棒,按如图 1 摆放时可摆成 m 个正方形,按如图 2摆放时可摆成 2n 个正方形.
(1)试分别用含 m,n 的代数式表示 a;
(2)若这 a 根火柴棒按如图 3 摆放时还可摆成 3p 个正方形.
①试问 p 的值能取 8 吗?请说明理由.
②试求 a 的最小值.
【答案】(1)a=3m+1,a=5n+2;(2)①a=3m+1,a=5n+2;②52.
【解析】
(1)观察图1发现,摆成1个正方形需要4根火柴棒,以后每多摆放1个正方形增加3根火柴棒,由此得出摆成m个正方形需要(3m+1)根火柴棒,即a=3m+1;同理得出用含n的代数式表示a的式子;
(2)①首先观察图3,得出用含p的代数式表示a的式子,把p=8代入求出a的值,再根据火柴棒的总数相同求出m、n即可判断;
②根据火柴棒的总数相同得出a=3m+1=5n+2=7p+3,求出最小正整数解,从而得到a的最小值.
解:(1)图 1 中火柴棒的总数是(3m+1)根,图 2 中火柴棒的总数是(5n+2)根,所以 a=3m+1,a=5n+2;
(2)∵图 3 中有 3p 个正方形,
∴火柴棒的总数是(7p+3)根.
①当 p=8 时,a=7×8+3=59,
如果3m+1=59,解得 m=![]() ,
,
如果5n+2=59,解得 n=![]() ,
,
m、n 的值都不是整数,不合题意, 所以 p 的值不能取 8;
②由题意得 a=3m+1=5n+2=7p+3,所以 p=![]() =
=![]() .
.
∵m,n,p 均是正整数,
∴m=17,n=10,p=7 时 a 的值最小,a=3×17+1=5×10+2=7×7+3=52.

练习册系列答案
相关题目