题目内容
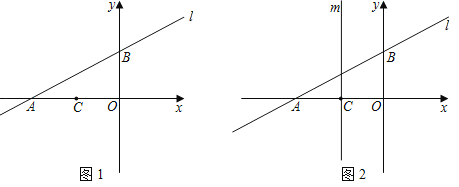
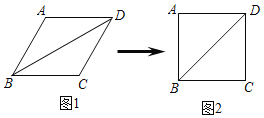
【题目】小明用四根长度相同的木条首尾相接制作了能够活动的学具,他先活动学具成为图1所示,并测得∠B=60°,接着活动学具成为图2所示,并测得∠ABC=90°,若图2对角线BD=40cm,则图1中对角线BD的长为( )
A.20cmB.20![]() cmC.20
cmC.20![]() cmD.20
cmD.20![]() cm
cm
【答案】D
【解析】
根据勾股定理即可求得正方形的边长,根据菱形的性质和勾股定理即可求得图1中BD的长.
∵AB=BC=CD=DA,
∴四边形ABCD是菱形(图1),
当∠ABC=90°时,四边形ABCD是正方形(图2),
∴图2中,∠A=90°,
∴AB2+AD2=BD2,
∴AB=AD=![]() BD=
BD=![]() cm,
cm,
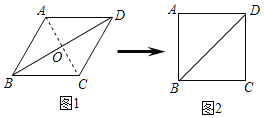
图1中,连接AC,交BD于O,
∵∠B=60°,四边形ABCD是菱形,
∴AC⊥BD,OB=OD,OA=OC,∠ABO=30°,
∴OA=![]() AB=10
AB=10![]() cm,OB=
cm,OB=![]() OA=10
OA=10![]() cm,
cm,
∴BD=2OB=20![]() cm;
cm;
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校兴趣小组以问卷调查的形式,随机调查了某地居民对武汉封城后续措施的了解情况,设置了多选题,并将调查结果绘制成如图不完整的统计图.
选项 | A | B | C | D | E |
后续措施 | 扩大宣传力度 | 分类隔离病人 | 封闭小区 | 聘请专业物资 | 采取其他措施 |
选择人次 | 25 | 85 | 15 | 35 |
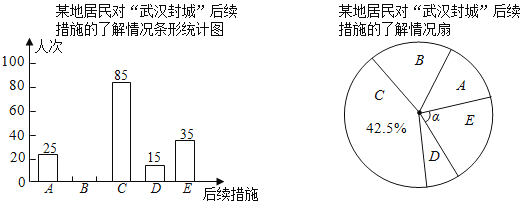
已知平均每人恰好选择了两个选项,根据以上信息回答下列问题:
(1)求参与本次问卷调查的居民人数,并补全条形统计图;
(2)在扇形统计图中,求E选项对应圆心角α的度数;
(3)根据此次调查结果估计该地100万居民当中选择D选项的人数.