题目内容
【题目】如图,等边![]() 的周长为1,作
的周长为1,作![]() 于
于![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() ;作
;作![]() 于
于![]() ,在
,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,连接
,连接![]() ,以
,以![]() 为边作等边
为边作等边![]() ;…且点
;…且点![]() ,
,![]() ,
,![]() ,…都在直线
,…都在直线![]() 同侧,如此下去,可得到
同侧,如此下去,可得到![]() 的边长为__________.(
的边长为__________.(![]() ,且
,且![]() 为整数)
为整数)
【答案】![]()
【解析】
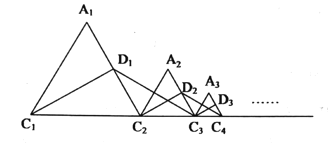
根据等边三角形的性质分别求出△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长即可解决问题.
∵等边△A1C1C2的周长为1,作C1D1⊥A1C2于D1,
∵C1D1=D1C3,
∴∠C1 C3D1=∠C3C1D1=30°,且∠C1 D1C2=90°
∴∠C2 D1C3=∠C1C3D1=30°
∴A1D1=D1C2= C2C3,
∴△A2C2C3的周长=![]() △A1C1C2的周长=
△A1C1C2的周长=![]() ,
,
∴△A1C1C2,△A2C2C3,△A3C3C4,…,△AnCnCn+1的周长分别为1,![]() ,
,![]() ,…,
,…,![]() ,
,
故答案为:![]() .
.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目