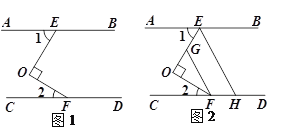题目内容
【题目】请将下列证明过程补充完整:
已知:如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2
求证:∠E=∠F

证明:∵∠BAP+∠APD=180°(已知)
∴ ∥ ( )
∴∠BAP= ( )
又∵∠1=∠2(已知)
∴∠BAP﹣ = ﹣∠2
即∠3= (等式的性质)
∴AE∥PF( )
∴∠E=∠F( )
【答案】答案见解析
【解析】分析:根据平行线的性质以及判定定理进行填空即可得出答案.
详解:∵∠BAP+∠APD=180°(已知)
∴ AB∥ CD(同旁内角互补,两直线平行 )
∴∠BAP= ∠APC (两直线平行,内错角相等 )
又∵∠1=∠2(已知)
∴∠BAP﹣ ∠1 = ∠APC ﹣∠2
即∠3= ∠4 (等式的性质)
∴AE∥PF(内错角相等,两直线平行 )
∴∠E=∠F(两直线平行,内错角相等 )

练习册系列答案
相关题目