题目内容
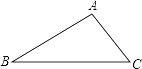
【题目】已知,如图所示,AB//CD,点E在AD的延长线上,∠EDC与∠B互为补角.
(1)问AD,BC是否平行?请说明理由;
(2)如果∠EDC=72°,∠1=∠2=2∠CAB,求∠CAF的度数.

【答案】(1)见解析;(2) 24°.
【解析】(1)根据AB//CD得∠DCB+∠B=180°,由∠EDC+∠B=180°,故可知∠EDC =∠DCB,从而求出结论;
(2)由∠EDC=72°,可求出∠B=108°,设∠CAB=x,则∠1=∠2=2x,在ABC中,由三角形同犯 定理可求出∠CAB=24°,由AB//CD得出∠BAF=48°,故可得出结论.
(1)AD//BC,
理由:
∵AB//CD,
∴∠DCB+∠B=180°,
又∵∠EDC与∠B互补,
∴∠EDC+∠B=180°
∴∠EDC =∠DCB,
∴AD//BC
(2)∵∠EDC=72°,
∴∠B=108°,
设∠CAB=x,则∠1=∠2=2x,
在ABC中,∠2 +∠CAB+∠B=180°,即x+2x+108=180,x=24°,
∵AB//CD,
∴∠BAF=∠1=48°,
∴∠CAF=∠BAF-∠BAC=24°

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目