题目内容
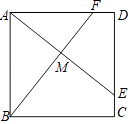
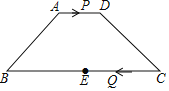
【题目】如图,在四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠CDA.
(1)求证:BE∥DF;
(2)若∠ABC=56°,求∠ADF的大小.

【答案】(1)证明见解析;(2)∠ADF=62°.
【解析】
(1)根据四边形的内角和定理和∠A=∠C=90°,得∠ABC+∠ADC=180°;根据角平分线定义、等角的余角相等易证明和BE与DF两条直线有关的一对同位角相等,从而证明两条直线平行;
(2)根据四边形的内角和和角平分线的定义即可得到结论.
(1)证明:∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°,
∵BE平分∠ABC,DF平分∠ADC,
∴∠1=∠2=![]() ∠ABC,∠3=∠4=
∠ABC,∠3=∠4=![]() ∠ADC,
∠ADC,
∴∠1+∠3=![]() (∠ABC+∠ADC)=
(∠ABC+∠ADC)=![]() ×180°=90°,
×180°=90°,
又∠1+∠AEB=90°,
∴∠3=∠AEB,
∴BE∥DF;
(2)解:∵∠ABC=56°,
∴∠ADC=360°﹣∠A﹣∠C﹣∠ABC=124°,
∵DF平分∠CDA,
∴∠ADF=![]() ∠ADC=62°.
∠ADC=62°.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目