题目内容
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( )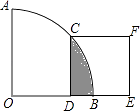
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
【答案】A
【解析】解:∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,
的中点,
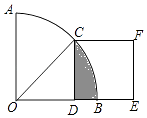
∴∠COD=45°,
∴OC= ![]() =4,
=4,
∴阴影部分的面积=扇形BOC的面积﹣三角形ODC的面积
= ![]() ×π×42﹣
×π×42﹣ ![]() ×(2
×(2 ![]() )2
)2
=2π﹣4.
所以答案是:A.
【考点精析】根据题目的已知条件,利用正方形的性质和扇形面积计算公式的相关知识可以得到问题的答案,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
【题目】下表是加热食用油的温度变化情况:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了110![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃B.加热50![]() ,油的温度是110℃
,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃D.每加热10![]() ,油的温度升高30℃
,油的温度升高30℃