题目内容
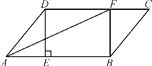
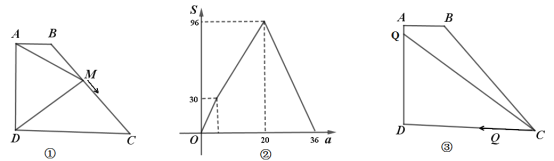
【题目】如图①,四边形![]() 中,
中,![]() .
.
(1)动点![]() 从
从![]() 出发,以每秒1个单位的速度沿路线
出发,以每秒1个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,
,![]() 的面积为
的面积为![]() 关于
关于![]() 的函数图象如图②所示,求
的函数图象如图②所示,求![]() 的长.
的长.
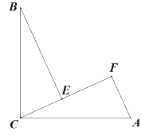
(2)如图③动点![]() 从点
从点![]() 出发,以每秒2个单位的速度沿路线
出发,以每秒2个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,同时,动点
停止,同时,动点![]() 从点
从点![]() 出发,以每秒5个单位的速度沿路线
出发,以每秒5个单位的速度沿路线![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,当
,当![]() 点运动到
点运动到![]() 边上时,连接
边上时,连接![]() ,当
,当![]() 的面积为8时,求
的面积为8时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() 和
和![]() .
.
【解析】
(1)根据题意由函数图象可知动点![]() 从
从![]() 出发,以每秒1个单位的速度从C到D耗时16秒求出CD,再利用三角形面积公式求得AD即可;
出发,以每秒1个单位的速度从C到D耗时16秒求出CD,再利用三角形面积公式求得AD即可;
(2)由题意可知只能有P和![]() 点都在
点都在![]() 边上,此时分当P在Q上方时以及当P在Q下方时两种情况运用数形结合思维进行分析得出答案.
边上,此时分当P在Q上方时以及当P在Q下方时两种情况运用数形结合思维进行分析得出答案.
解:(1)由函数图象可知动点![]() 从
从![]() 出发,以每秒1个单位的速度从C到D耗时36-20=16秒,即CD=16,而此时
出发,以每秒1个单位的速度从C到D耗时36-20=16秒,即CD=16,而此时![]() 的面积为96,又因为
的面积为96,又因为![]() ,
,
即有![]() ,解得
,解得![]() .
.
所以![]() .
.
(2)由题意可知Q运动到点![]() 停止的时间为
停止的时间为![]() ,而P运动到点
,而P运动到点![]() 停止的时间为6,
停止的时间为6,
所以只能有P和![]() 点都在
点都在![]() 边上,此时以PQ为底边,CD为高,
边上,此时以PQ为底边,CD为高,
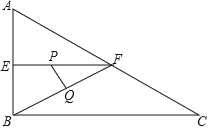
设运动时间为![]() ,则AP=2t,QD=5t-16,(
,则AP=2t,QD=5t-16,(![]() ),
),
①当P在Q上方时,则有PQ=AD-AP-QD= ![]() ,
,
可知![]() 的面积为8时即
的面积为8时即![]() ,解得
,解得![]() (满足条件);
(满足条件);
②当P在Q下方时,则有PQ=QD-(AD-AP)= ![]() ,
,
可知![]() 的面积为8时即
的面积为8时即![]() ,解得
,解得![]() (满足条件).
(满足条件).
所以当![]() 的面积为8时,
的面积为8时,![]() 的值为
的值为![]() 和
和![]() .
.

练习册系列答案
相关题目
【题目】下表是加热食用油的温度变化情况:
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现,烧了110![]() 时,油沸腾了,则下列说法不正确的是( )
时,油沸腾了,则下列说法不正确的是( )
A.没有加热时,油的温度是10℃B.加热50![]() ,油的温度是110℃
,油的温度是110℃
C.估计这种食用油的沸点温度约是230℃D.每加热10![]() ,油的温度升高30℃
,油的温度升高30℃