Question

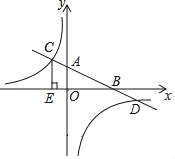
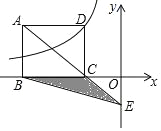
【题目】如图所示，矩形ABCD的顶点D在反比例函数（x＜0）的图象上，顶点B，C在x轴上，对角线AC的延长线交y轴于点E，连接BE，△BCE的面积是6，则k=_____．

Answer 1

【答案】-12

【解析】

先设D（a，b），得出CO=-a，CD=AB=b，k=ab，再根据△BCE的面积是6，得出BC×OE=12，最后根据AB∥OE，得出，即BCEO=ABCO，求得ab的值即可．

设D（a，b），则CO=-a，CD=AB=b，

∵矩形ABCD的顶点D在反比例函数y=（x＜0）的图象上，

∴k=ab，

∵△BCE的面积是6，

∴×BC×OE=6，即BC×OE=12，

∵AB∥OE，

∴，即BCEO=ABCO，

∴12=b×（-a），即ab=-12，

∴k=-12，

故答案为：-12．