题目内容
【题目】(阅读理解)利用完全平方公式,可以将多项式![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:![]()
![]()
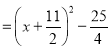
![]()
![]()
(问题解决)根据以上材料,解答下列问题:
(1)用多项式的配方法将多项式![]() 化成
化成![]() 的形式;
的形式;
(2)用多项式的配方法及平方差公式对多项式![]() 进行分解因式;
进行分解因式;
(3)求证:不论![]() ,
,![]() 取任何实数,多项式
取任何实数,多项式![]() 的值总为正数.
的值总为正数.
【答案】(1)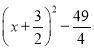 ,见解析;(2)
,见解析;(2)![]() ,见解析;(3)见解析
,见解析;(3)见解析
【解析】
(1)根据题中给出的例题,利用完全平方公式进行配方即可;
(2)根据题中给出的例题,利用完全平方公式进行配方后,再利用平方差公式进行因式分解即可;
(3)利用配方法将多项式化成![]() 后,再结合平方的非负性即可求证.
后,再结合平方的非负性即可求证.
解:(1) ![]()
![]()
![]()
(2)由(1)得![]()
![]()
![]()
![]() .
.
(3)![]()
![]()
![]()
![]() ,
,![]()
![]() ,
,
![]() 不论
不论![]() ,
,![]() 取任何实数,多项式
取任何实数,多项式![]() 的值总为正数.
的值总为正数.

练习册系列答案
相关题目
【题目】某中学举行“中国梦·校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如下图所示:

根据图示信息,整理分析数据如下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(说明:图中虚线部分的间隔距离均相等)
(1)求出表格中![]() 的值;
的值;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.