题目内容
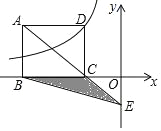
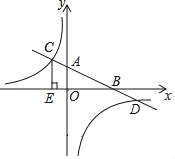
【题目】已知:如图,在平面直角坐标系xOy中,直线AB分别与x轴、y轴交于点B,A,与反比例函数的图象分别交于点C,D,CE⊥x轴于点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求该反比例函数的解析式;
(2)求三角形CDE的面积.
【答案】(1)![]() ;(2)12.
;(2)12.
【解析】
(1)根据正切的定义求出OA,证明△BAO∽△BEC,根据相似三角形的性质计算;
(2)求出直线AB的解析式,解方程组求出点D的坐标,根据三角形CDE的面积=三角形CBE的面积+三角形BED的面积计算即可.
解:(1)∵tan∠ABO=![]() ,OB=4,
,OB=4,
∴OA=2,
∵OE=2,
∴BE=6,
∵AO∥CE,
∴△BAO∽△BEC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,CE=3,即点C的坐标为(﹣2,3),
∴反比例函数的解析式为:![]() ;
;
(2)设直线AB的解析式为:y=kx+b,
则![]() ,
,
解得,![]() ,
,
则直线AB的解析式为:![]() ,
,
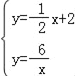 ,
,
解得,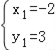 ,
,![]() ,
,
∴当D的坐标为(6,1),
∴三角形CDE的面积=三角形CBE的面积+三角形BED的面积
=![]() ×6×3+
×6×3+![]() ×6×1
×6×1
=12.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目