题目内容
如图,正方形ABCD的边长为2,点E是BC边的中点,过点B作BG⊥AE,
垂足为G,延长BG交AC于点F,则CF= .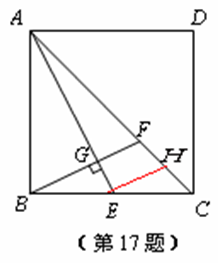
垂足为G,延长BG交AC于点F,则CF= .


延长BF交CD于H.根据勾股定理求得AC的长,根据ASA可以证明△ABE≌△BCH,则CH=BE=1,再根据相似三角形的性质解.
解:延长BF交CD于H.

在正方形ABCD中,正方形的边长是2,根据勾股定理,得AC=2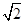 .
.
∵AB=BC,∠ABE=∠BCH=90°,∠BAE=∠CBH,
∴△ABE≌△BCH,
∴CH=BE=1.
∵AB∥CD,
∴△ABF∽△CHF,
∴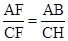 =2,
=2,
∴CF=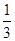 AC=
AC= .
.
故答案为 .
.
解:延长BF交CD于H.

在正方形ABCD中,正方形的边长是2,根据勾股定理,得AC=2
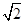 .
.∵AB=BC,∠ABE=∠BCH=90°,∠BAE=∠CBH,
∴△ABE≌△BCH,
∴CH=BE=1.
∵AB∥CD,
∴△ABF∽△CHF,
∴
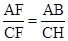 =2,
=2,∴CF=
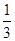 AC=
AC= .
.故答案为
 .
.
练习册系列答案
相关题目
 .
.
 中选择两个条件________(用序号表示,只填一种情况),使得
中选择两个条件________(用序号表示,只填一种情况),使得 ,并加以证明.
,并加以证明.
 的边长为2, 将长为2的线段
的边长为2, 将长为2的线段 的两端放在正方形相邻的
的两端放在正方形相邻的 从点
从点 出发,沿图中所示方向按
出发,沿图中所示方向按 滑动到点
滑动到点 从点
从点 出发,沿图中所示方向按
出发,沿图中所示方向按 滑动到点
滑动到点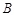 为止,那
为止,那 的中点
的中点 所经过的路线围成的图形的面积为
所经过的路线围成的图形的面积为 




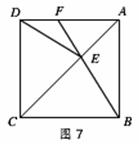
 求四边形AEBD的面积.(5分)
求四边形AEBD的面积.(5分)
