题目内容
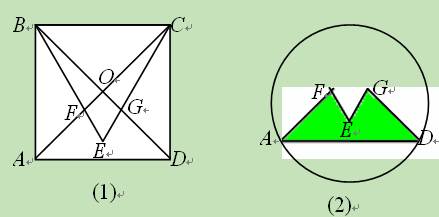
(本题满分8分)已知矩形ABCD的对角线相交于点O,M 、N分别是OD、OC上异于O、C、D的点。
(1)请你在下列条件①DM=CN,②OM=ON,③MN是△OCD的中位线,④MN∥AB中任选一个添加条件(或添加一个你认为更满意的其他条件),使四边形ABNM为等腰梯形,你添加的条件是 。
(2)添加条件后,请证明四边形ABNM是等腰梯形。
(1)请你在下列条件①DM=CN,②OM=ON,③MN是△OCD的中位线,④MN∥AB中任选一个添加条件(或添加一个你认为更满意的其他条件),使四边形ABNM为等腰梯形,你添加的条件是 。
(2)添加条件后,请证明四边形ABNM是等腰梯形。

(1)选择①DM=CN
(2)证明:∵AD=BC,∠ADM=∠BCN,DM=CN
∴△AND≌△BCN,∴AM=BN,由OD=OC知OM=ON,∴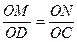 ∴MN∥CD∥AB,且MN≠AB ∴四边形ABNM是等腰梯形。
∴MN∥CD∥AB,且MN≠AB ∴四边形ABNM是等腰梯形。
(2)证明:∵AD=BC,∠ADM=∠BCN,DM=CN
∴△AND≌△BCN,∴AM=BN,由OD=OC知OM=ON,∴
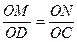 ∴MN∥CD∥AB,且MN≠AB ∴四边形ABNM是等腰梯形。
∴MN∥CD∥AB,且MN≠AB ∴四边形ABNM是等腰梯形。略

练习册系列答案
相关题目

 AB,
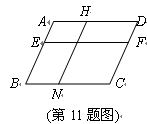
AB, ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒
ABCD的面积是2,AB=a,BC=b,点E从点A出发沿AB以每秒v个单位长的速度向点B运动,点F从点B出发沿BC以每秒 个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
个单位长的速度向点C运动.E、F分别从点A、B同时出发,当其中一点到达端点时,另一点也随之停止运动.请问四边形DEBF的面积的值是否随着时间t的变化而变化?若不变,请写出这个值 ,并写出理由;若变化,说明是怎样变化的.
 与AD重合,由旋转可得:
与AD重合,由旋转可得: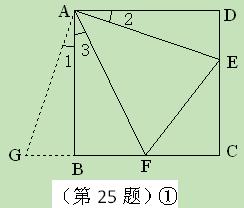
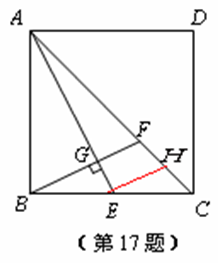
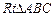 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=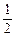 ∠DAB.试猜想DE,BF,EF之间有何数量
∠DAB.试猜想DE,BF,EF之间有何数量 关系,并证明你的猜想.
关系,并证明你的猜想.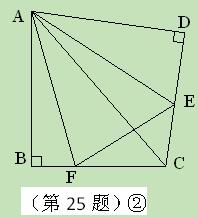
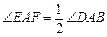 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
 且BE=FC,连接DE,AF.求证:DE=AF.
且BE=FC,连接DE,AF.求证:DE=AF.
