题目内容
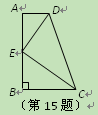
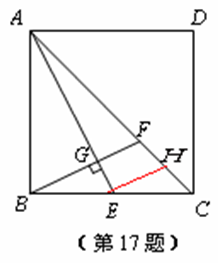
(2011•重庆)如图,梯形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.
(1)求EG的长;
(2)求证:CF=AB+AF.
(1)求EG的长;
(2)求证:CF=AB+AF.

(1)解:∵BD⊥CD,∠DCB=45°,
∴∠DBC=45°=∠DCB,∴BD=CD=2,在Rt△BDC中BC= =2
=2 ,∵CE⊥BE,点G为BC的中点,∴EG=
,∵CE⊥BE,点G为BC的中点,∴EG= BC=
BC= .
.
答:EG的长是 .
.
(2)证明:在线段CF上截取CH=BA,连接DH,
∵BD⊥CD,BE⊥CE,

∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°
∵∠EFB=∠DFC,
∴∠EBF=∠DCF,
∵DB=CD,BA=CH,
∴△ABD≌△HCD,
∴AD=DH,∠ADB=∠HDC,
∵AD∥BC,
∴∠ADB=∠DBC=45°,
∴∠HDC=45°,∴∠HDB=∠BDC﹣∠HDC=45°,
∴∠ADB=∠HDB,
∵AD=HD,DF=DF,
∴△ADF≌△HDF,
∴AF=HF,
∴CF=CH+HF=AB+AF,
∴CF=AB+AF.
∴∠DBC=45°=∠DCB,∴BD=CD=2,在Rt△BDC中BC=
 =2
=2 ,∵CE⊥BE,点G为BC的中点,∴EG=
,∵CE⊥BE,点G为BC的中点,∴EG= BC=
BC= .
.答:EG的长是
 .
.(2)证明:在线段CF上截取CH=BA,连接DH,
∵BD⊥CD,BE⊥CE,

∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°
∵∠EFB=∠DFC,
∴∠EBF=∠DCF,
∵DB=CD,BA=CH,
∴△ABD≌△HCD,
∴AD=DH,∠ADB=∠HDC,
∵AD∥BC,
∴∠ADB=∠DBC=45°,
∴∠HDC=45°,∴∠HDB=∠BDC﹣∠HDC=45°,
∴∠ADB=∠HDB,
∵AD=HD,DF=DF,
∴△ADF≌△HDF,
∴AF=HF,
∴CF=CH+HF=AB+AF,
∴CF=AB+AF.
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
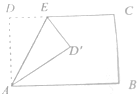
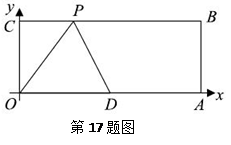


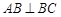 ,
,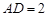 ,
,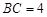 ,点E在AB边上,且CE平分
,点E在AB边上,且CE平分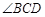 ,DE平分
,DE平分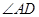 ,则点E到CD的距离为 .
,则点E到CD的距离为 .