题目内容
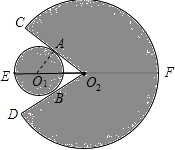
【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm. 
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2 , 当⊙O1的半径为多少时,该玩具的制作成本最小?
【答案】
(1)解:连接O1A.
∵⊙O1与O2C、O2D分别切一点A、B
∴O1A⊥O2C,O2E平分∠CO2D,
∴∠AO2O1= ![]() ∠CO2D=30°,
∠CO2D=30°,
∴在Rt△O1AO2中,O1O2=2AO1=2x.
∴FO2=EF﹣EO1﹣O1O2=24﹣3x,即扇形O2CD的半径为(24﹣3x)cm
(2)解:设该玩具的制作成本为y元,则
y=0.45πx2+0.06× ![]()
=0.9πx2﹣7.2πx+28.8π
=0.9π(x﹣4)2+14.4π
所以当x﹣4=0,即x=4时,y的值最小.
答:当⊙O1的半径为4cm时,该玩具的制作成本最小.
【解析】(1)连接O1A.利用切线的性质知∠AO2O1= ![]() ∠CO2D=30°;然后在Rt△O1AO2中利用“30°角所对的直角边是斜边的一半”求得O1O2=2x;最后由图形中线段间的和差关系求得扇形O2CD的半径FO2为:EF﹣EO1﹣O1O2=24﹣3x;(2)设该玩具的制作成本为y元,则根据圆形的面积公式和扇形的面积公式列出y与x间的函数关系,然后利用二次函数的最值即可求得该玩具的最小制作成本.
∠CO2D=30°;然后在Rt△O1AO2中利用“30°角所对的直角边是斜边的一半”求得O1O2=2x;最后由图形中线段间的和差关系求得扇形O2CD的半径FO2为:EF﹣EO1﹣O1O2=24﹣3x;(2)设该玩具的制作成本为y元,则根据圆形的面积公式和扇形的面积公式列出y与x间的函数关系,然后利用二次函数的最值即可求得该玩具的最小制作成本.
【考点精析】认真审题,首先需要了解二次函数的最值(如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a),还要掌握切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径)的相关知识才是答题的关键.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案【题目】某中学七年级学生共450人,其中男生250人,女生200人.该校对七年级所有学生进行了一次体育测试,并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表:
成绩 | 划记 | 频数 | 百分比 |
不及格 |
| 9 | 10% |
及格 |
| 18 | 20% |
良好 |
| 36 | 40% |
优秀 |
| 27 | 30% |
合计 | 90 | 90 | 100% |
(1)请解释“随机抽取了50名男生和40名女生”的合理性;
(2)从上表的“频数”,“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校七年级体育测试成绩不及格的人数.