题目内容
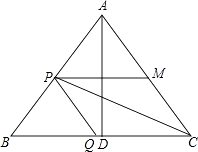
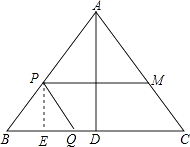
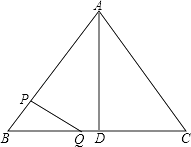
【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.
(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形. ①若a= ![]() ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.
【答案】
(1)解:△ABC中,AB=AC=10cm,BC=12cm,D是BC的中点,
∴BD=CD= ![]() BC=6cm,
BC=6cm,
∵a=2,
∴BP=2tcm,DQ=tcm,
∴BQ=BD﹣QD=6﹣t(cm),
∵△BPQ∽△BDA,
∴ ![]() ,
,
即 ![]() ,
,
解得:t= ![]()
(2)解:①过点P作PE⊥BC于E,
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,
∴PB=CM,
∴PB=PQ,
∴BE= ![]() BQ=
BQ= ![]() (6﹣t)cm,
(6﹣t)cm,
∵a= ![]() ,
,
∴PB= ![]() tcm,
tcm,
∵AD⊥BC,
∴PE∥AD,
∴PB:AB=BE:BD,
即 ![]() ,
,
解得:t= ![]() ,
,
∴PQ=PB= ![]() t=
t= ![]() (cm);
(cm);
②不存在.理由如下:
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,∴PB=CM,∴PB=PQ.
若点P在∠ACB的平分线上,则∠PCQ=∠PCM,
∵PM∥CQ,
∴∠PCQ=∠CPM,
∴∠CPM=∠PCM,
∴PM=CM,
∴四边形PQCM是菱形,
∴PQ=CQ,PM∥CQ,
∴PB=CQ,PM:BC=AP:AB,
∵PB=atcm,CQ=CD+QD=6+t(cm),
∴PM=CQ=6+t(cm),AP=AB﹣PB=10﹣at(cm),
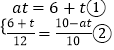 ,
,
化简得②:6at+5t=30③,
把①代入③得,t=﹣ ![]() ,
,
∴不存在实数a,使得点P在∠ACB的平分线上.
【解析】(1)由△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,根据等腰三角形三线合一的性质,即可求得BD与CD的长,又由a=2,△BPQ∽△BDA,利用相似三角形的对应边成比例,即可求得t的值;(2)①首先过点P作PE⊥BC于E,由四边形PQCM为平行四边形,易证得PB=PQ,又由平行线分线段成比例定理,即可得方程 ![]() ,解此方程即可求得答案;②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.
,解此方程即可求得答案;②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.

 阅读快车系列答案
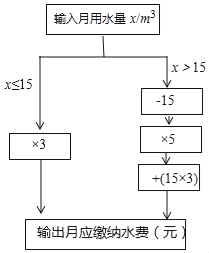
阅读快车系列答案【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.