题目内容
【题目】直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:分别过点A、B、D作AF⊥l3 , BE⊥l3 , DG⊥l3 , 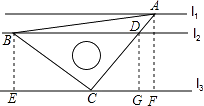
∵△ABC是等腰直角三角形,
∴AC=BC,
∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,
∴∠EBC=∠ACF,∠BCE=∠CAF,
在△BCE与△ACF中,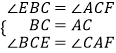 ,
,
∴△BCE≌△ACF(ASA)
∴CF=BE,CE=AF,
∵l1与l2的距离为1,l2与l3的距离为3,
∴CF=BE=3,CE=AF=3+1=4,
在Rt△ACF中,
∵AF=4,CF=3,
∴AC= ![]() =
= ![]() =5,
=5,
∵AF⊥l3 , DG⊥l3 ,
∴△CDG∽△CAF,
∴ ![]() ,
, ![]() =
= ![]() ,解得CD=
,解得CD= ![]() ,
,
在Rt△BCD中,
∵CD= ![]() ,BC=5,
,BC=5,
∴BD= ![]() =
= ![]() =
= ![]() .
.
故选A.
【考点精析】利用等腰直角三角形和平行线之间的距离对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目