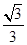题目内容
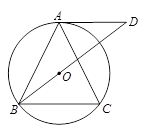
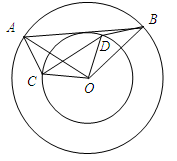
如图,⊙O是△ABC的外接圆,AB=AC,过点A作AD∥BC交BO的延长线于点D.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径OB=5,BC=8,求线段AD的长.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径OB=5,BC=8,求线段AD的长.

(1)证明见解析;(2)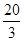 .
.
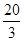 .
.试题分析:(1)连接AO,并延长交⊙O于E,交BC于F,由题意可知AE⊥BC且AB=AC,得出AE经过圆心O,只要证明AD⊥AE即可.
(2)可通过△AOD∽△FOB及勾股定理求出AD的长.
(1)如图,连接AO,并延长交⊙O于E,交BC于F.
∵AB=AC,∴
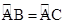 .∴
.∴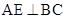 .∴
.∴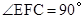 .
.∵AD∥BC,∴
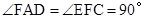 ,即AD⊥AE.
,即AD⊥AE.∵AO是半径,∴AD是⊙O的切线.
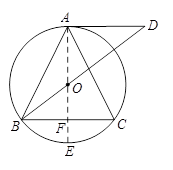
(2)∵AE是直径,
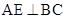 ,BC=8,∴
,BC=8,∴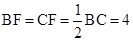 .
.∵OB=5,∴
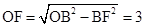 .
.∵AD∥BC,∴△AOD∽△FOB.∴
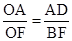 .
.∴
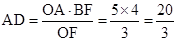 .
.
练习册系列答案
相关题目

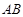 、
、 相交于点
相交于点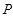 , 若
, 若 ,
,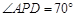 ,则
,则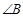 等于 .
等于 .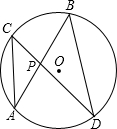

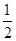 B.
B.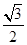 C.
C.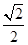 D.
D.