题目内容
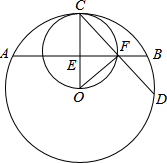
如图,两个同心圆的圆心为O,两圆的半径分别为5,3,其中A,B两点在大圆上,C,D在小圆上,且∠AOB=∠COD.
(1)求证:AC=BD;
(2)若∠AOB=120°,求线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积;
(3)若AB与小圆相切,分别求AB,CD的长.
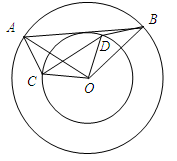
(1)求证:AC=BD;
(2)若∠AOB=120°,求线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积;
(3)若AB与小圆相切,分别求AB,CD的长.

(1)证明见解析;(2)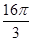 ;(3)8,
;(3)8,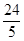 .
.
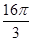 ;(3)8,
;(3)8,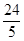 .
.试题分析:(1)如要证明AC=BD,则通过可证明△AOC≌△BOD即可;
(2)由题意可知线段AC,弧CD,线段BD,弧AB组成的封闭图形的面积,即为扇形AOB的面积,即为△ACO绕O旋转120度后,AC扫过的面积;
(3)切点为E,连接OE,首先利用勾股定理可求出BE的长,进而求出AB的长,再证明△AOC∽△BOD,利用相似三角形的性质即可求出CD的长.
(1)证明:在△AOC和△BOD中,
∵∠AOB=∠COD
∴∠AOC=∠BOD
∵OA=OB,OC=OD
∴△AOC≌△BOD,
∴ AC=BD.
(2)封闭图形的面积=
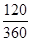 ×16
×16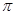 =
=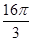 .
.(3)解:设切点为E,连接OE,
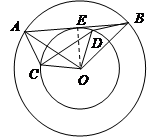
∵AB与小圆相切,
∴OE⊥AB,AB=2BE
由勾股定理得,BE=4,
∴AB=8.
∵∠AOB=∠COD,
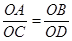 ,
,∴△AOC∽△BOD,
∴
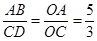
∴CD=
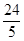 .
. 
练习册系列答案
相关题目
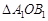 .
.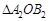 ,并判断
,并判断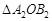 在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.
在位置上有何关系?若成中心对称,请直接写出对称中心坐标;如成轴对称,请直接写出对称轴的函数关系式.